Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
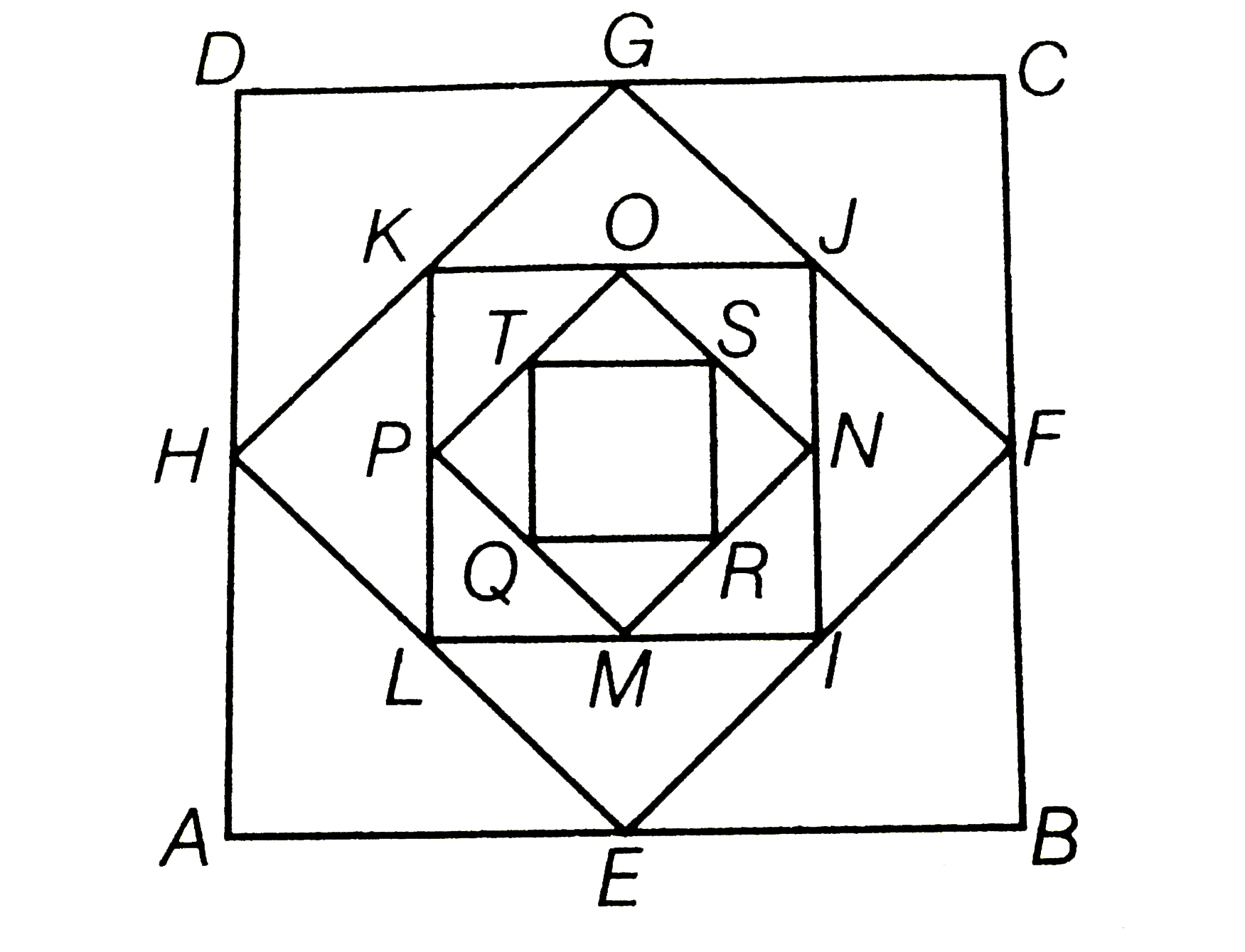
- A square is drawn by joining mid pint of the sides of a square. Anothe...
Text Solution
|
- A square is drawn by joining the mid-points of the sides of a square. ...
Text Solution
|
- Prove that the sum of the areas of the squares drawn on the sides of a...
Text Solution
|
- एक वर्ग की एक भुजा 10 सेमी है । भुजाओं के मध्य बिंदुओं को मिलाकर ए...
Text Solution
|
- A square is drawn by joining the mid points of the sides of a square. ...
Text Solution
|
- In the figure shown square II is formed by joining the mid-points of ...
Text Solution
|
- In the figure shown square II is formed by joining the mid-points of ...
Text Solution
|
- A square is drawn by joining the mid points of the sides of a given sq...
Text Solution
|
- A square is drawn by joining the mid-points of the sides of a square. ...
Text Solution
|
 .
.