Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
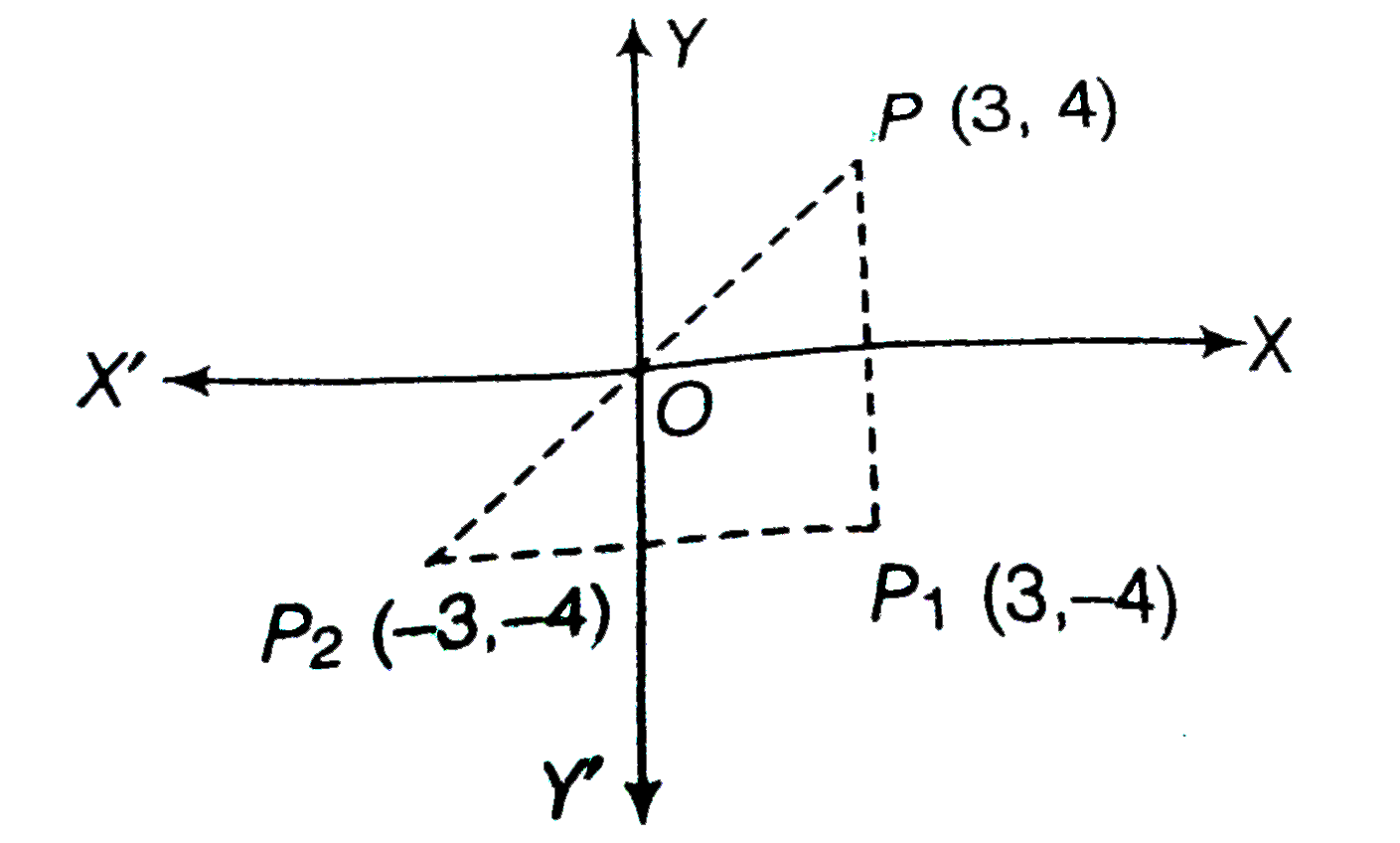
- The point p(3,4) undergoes a reflection in the X-axis followed by a r...
Text Solution
|
- If points Q and R reflections of point P(-3,\ 4) in X and Y axes ...
Text Solution
|
- A ray of light leave the point (3,4) reflects off the y-axis towards x...
Text Solution
|
- Find the reflection of a point (3,4) in line x=-2
Text Solution
|
- A point P is reflected in the x - axis . Co - ordinates of its image a...
Text Solution
|
- A point P is reflected in the x-axis. Co-ordinates of its image are (-...
Text Solution
|
- A point P is reflected in the origin. Co-ordinates of its image are (-...
Text Solution
|
- The point P(a, b) is first reflected in the origin and then reflected ...
Text Solution
|
- The point P(x, y) is first reflected in the x-axis and then reflected ...
Text Solution
|