Electric field due to an electric dipole at points on the axial line : Consider an electric dipole placed on the x-axis. A point C is located at a distance of r from the midpoint O (of the dipole) along the axial line.
` `
The eletctric field at a point C due to +q is
`vec(E)=(1)/(4piepsi_(0))(q)/((r-a)^(2))` along BC
Since the electric dipole moment vector `vec(p)` is from -q to +q and is directed along BC, the above equation is rewritten as
`vec(E)=(1)/(4piepsi_(0))(q)/((r-a)^(2))hatp" ".......(1)`
where `vec(p)` is the electric dipole moment unit vector from -q to +q. The electric field at a point C due to -q is
`vec(E)=-(1)/(4piepsi_(0))(q)/((r+a)^(2))hatp" ".......(2)`
Since +q is located closer to the point C than `-q,vec(E)_(+)` is stronger tham `vec(E)_(-)`. Therefore, the length of the `vec(E)_(+)` vector is drawn larger than that of `vec(E)_(-)` vector.
The total electric field at point C is calculated using the superposition principle of the electric field.
`vec(E)_("tot")=vec(E)_(+)+vec(E)_(-)`
`=(1)/(4piepsi_(0))(q)/((r-a)^(2))hatp-(1)/(4piepsi_(0))(q)/((r+a)^(2))hatp" "......(3)`
`vec(E)_("tot")=(q)/(4piepsi_(0))((1)/((r-a)^(2))-(1)/((r+a)^(2)))hatp" ".......(4)`
`vec(E)_("tot")=(1)/(4piepsi_(0))q((4ra)/((r^(2)-a^(2))))hatp" "......(5)`
Note that the total electric field is along `vec(E)_(+)` since +q is closer to C than -q.
If the point C is very far away from the dipole then `(rgtgta)`. Under this limit the term `(r^(2)-a^(2))~~r^(2)`. Substituting this
`vec(E)_("tot")=(1)/(4piepsi_(0))((4aq)/(r^(3)))hatp(rgtgta)`
Since `2aqhatp=vec(p)`
`vec(E)_("tot")=(1)/(4piepsi)(2vec(p))/(r^(3))(rgtgta)" "......(6)`
The direction of `vec(E)_("tot")` is shown in Figure.

Total electric of the dipole on the axial line
If the point C is chosen on the left side of the dipole, the total electric field is still in the direction of `vec(p)`.
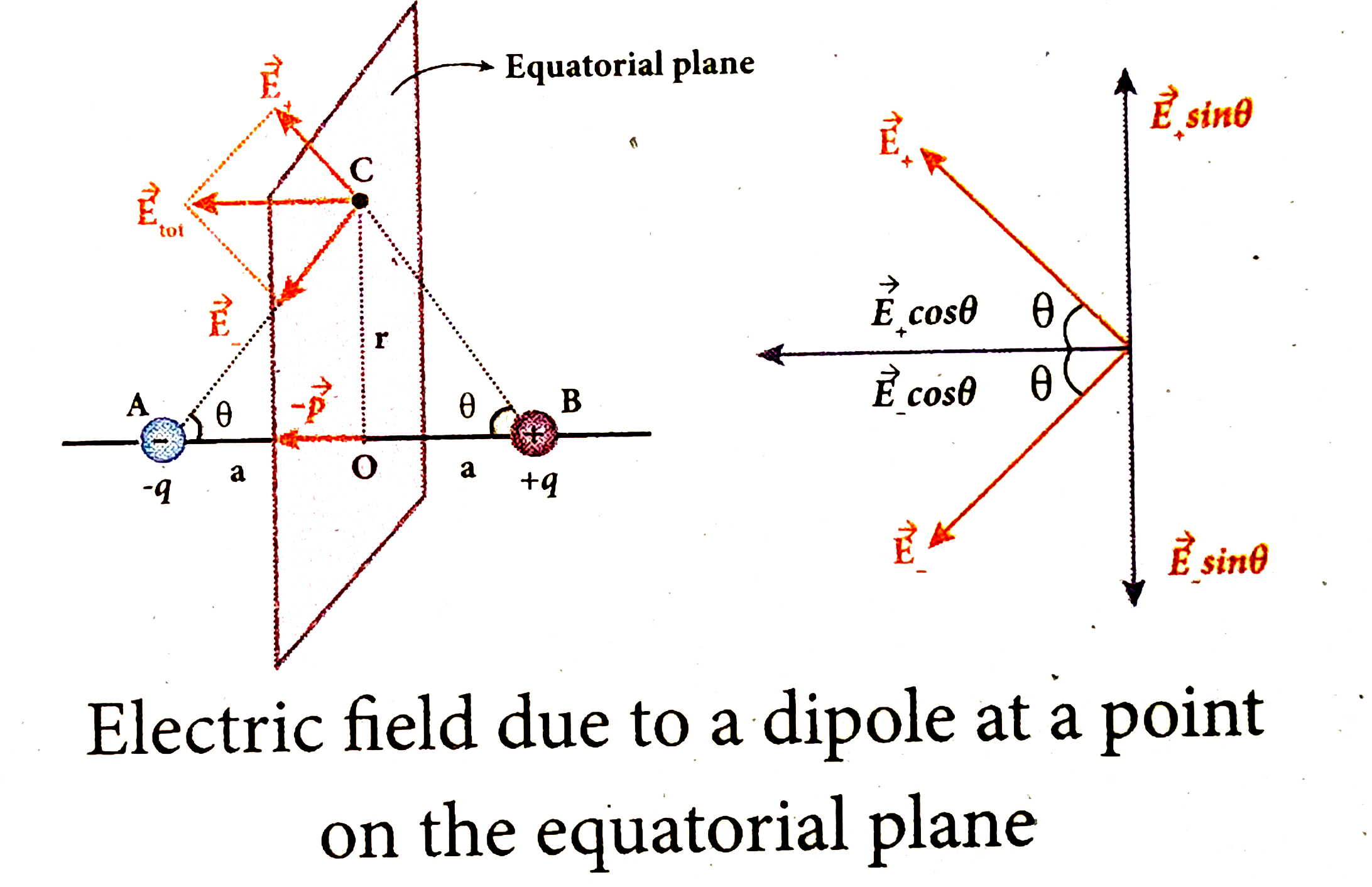
Electric field due to to dipole at a point on the equatorial plane
Electric field due to an electric dipole at a point on the equatroial plane :
Consider a point C at a distance r from the midpoint O of the dipole on the equatorial plane.
(ii) Since the point C is equi-distant from +q and -q, the magnitude of the electric fields of +q and -q are the same. The direction of `vec(E)_(+)` is along BC and the direction of `vec(E)_(-)` is along CA. `vec(E)_(+)andvec(E)_(-)` are resolved into two components, one component parallel to the dipole axis and the other perpendicular to it. The perpendicular components `|vec(E)_(+)|sinthetaand|vec(E)_(-)|sintheta` are oppositely directed and cancel each other. The magnitude of the total electric field at point C is the sum of the parallel components of `vec(E)_(+)andvec(E)_(-)` and its direction is along -p as shown in the Figure.
`vec(E)_("tot")=|vec(E)_(+)|costhetahatp-|vec(E)_(-)|costhetahatp" "......(1)`
The magnitudes `vec(E)_(+)andvec(E)_(-)` are the same and are given by
`|vec(E)_(+)|=|vec(E)_(-)|=(1)/(4piepsi_(0))=(q)/((r^(2)+a^(2)))" ".......(2)`
By substituting equation (2) into equation (1), we get
`vec(E)_("tot")=(1)/(4piepsi_(0))(2qcostheta)/((r^(2)+a^(2)))hatp`
`=(1)/(4piepsi_(0))(2qcostheta)/((r^(2)+a^(2))^(3/2))hatp`
Since `costheta=(a)/(sqrt(r^(2)+a^(2)))`
`vec(E)_("tot")=(1)/(4piepsi_(0))(vec(p))/((r^(2)+a^(2))^(3/2))`
since `vec(p)=2qahatp" ".......(3)`
At very large distances `(rgtgta)`, the equation (3) becomes
`vec(E)_("tot")=-(1)/(4piepsi_(0))(vec(p))/(r^(3))" "(rgtgta)`
(iii) The magnitude of the electric field at points on the dipole axis is twice the magnitude of the electric field at points on the equatorial plane. The direction of the electric field at points on the dipole axis is directed along the driection of dipole moment vector `-vec(p)` but at points on the equatorial plane it is directed oppsite to the dipole moment vector, that is along `-vec(p)` .
(iv) At very large distances, the electric field due to a dipole varies as `(1)/(r^(3))` for a point charge, the electric field varies as `(1)/(r^(2))`. Electric field due to a dipole at very large distances E goes to zero faster than the electric field due to a point charge.
(v) `vec(E)=(1)/(4piepsi_(0))(vecp)/(r^(3))` valid only at very large distances `(rgtgta)`.

