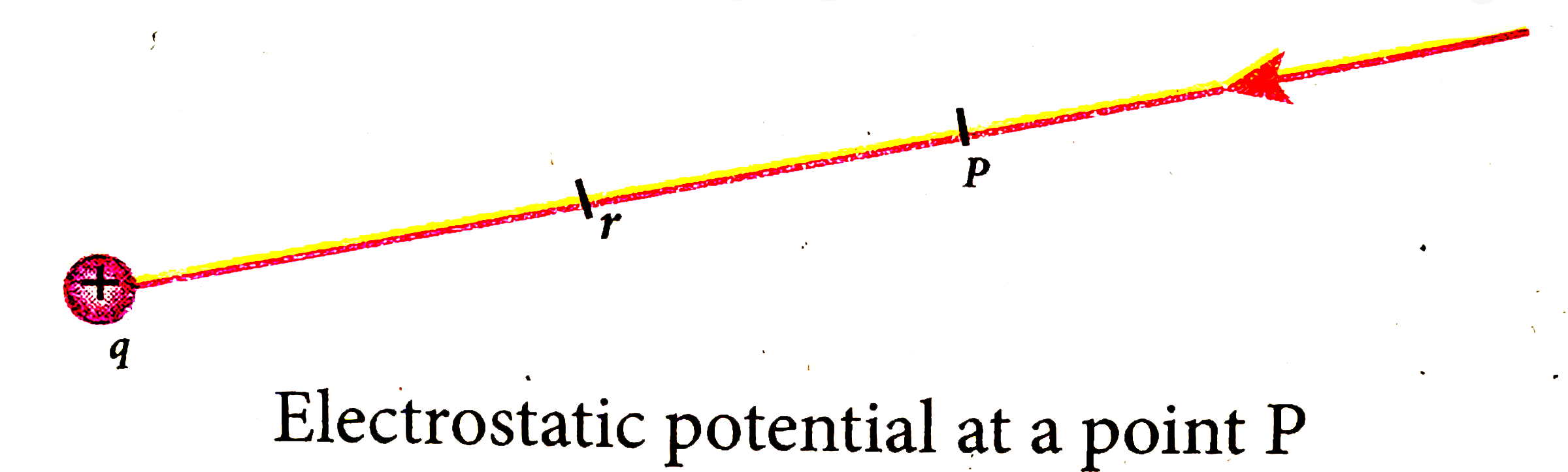Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Derive an expression for electrostatic potential due to a point charge...
Text Solution
|
- Derive an expression for the electric potential due to a point charge.
Text Solution
|
- Derive an expression for the electrostatic potential energy of a syste...
Text Solution
|
- किसी बिंदु आवेश के कारण किसी बिंदु पर विद्युत् विभव का व्यंजक व्युत्पन...
Text Solution
|
- Derive an expression for electrostatic potential due to an electric di...
Text Solution
|
- Derive an expression for electrostatic potential due to a point charge...
Text Solution
|
- Derive an expression for electrostatic potential due to an electric di...
Text Solution
|
- Derive an expression for electrostatic potential due to an electric di...
Text Solution
|
- electrostatic Potential|potential due to a point charge
Text Solution
|