The electric potential at a distance r from point charge `q_(1)` is given by
`V=(1)/(4piepsi_(0))(q_(1))/(r)`
(ii) This potential V is the work done to bring a unit positive chrage from infinity to the point. Now if the charge `q_(2)` is brought from infinity to that point at distance r from `q_(1)`, the work done is the product of `q_(2)` and the electric potential at that point. Thus we have
`W=q_(2)V`
(iii) This work done is stored as the electrostatic potential energy U of a system of charges `q_(1)andq_(2)` separated by a distance r. Thus we have
`U=q_(2)V=(1)/(4piepsi_(0))(q_(1)q_(2))/(r)" ".......(1)`
(iv) Three charges are arranged in the following configuration as shown in Figure.
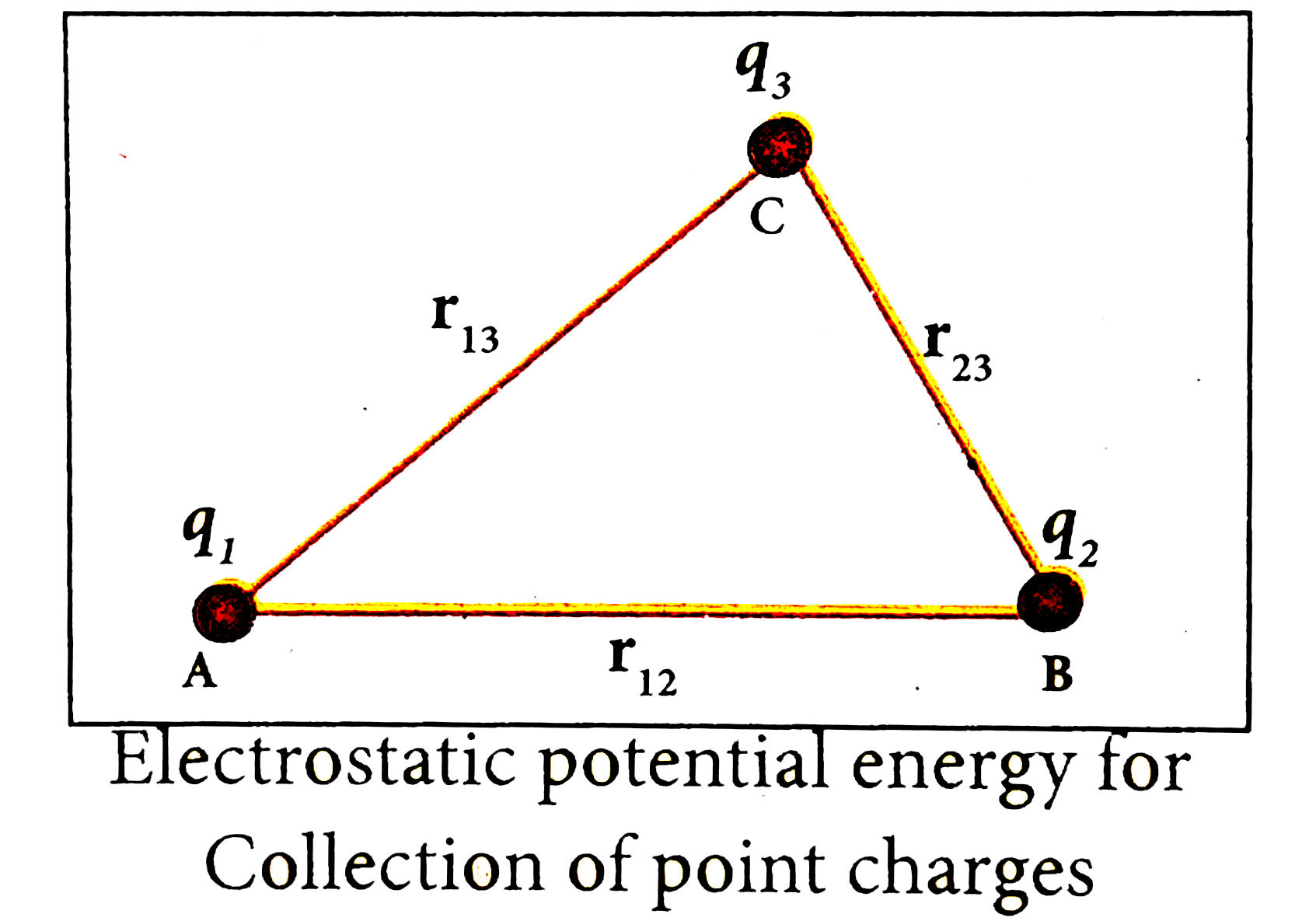
(a) Bringing a charge `q_(1)` from infinity to the point A requires no work, because there are no other charges already present in the vicinity of charge `q_(1)`.
(b) To bring the second charge `q_(2)` to the point B, work must be done aganist the electric field at B created by the charge `q_(1)`. So the work doen on the charge `q_(2)` is `W=q_(2)V_(1B)`. Here `V_(1B)` is the electrostatic potential due to the charge `q_(1)` at point B.
`U=(1)/(4piepsi_(0))(q_(1)q_(2))/(r_(12))" ".........(2)`
(c) Similarly to bring the charge `q_(3)` to the point C, work has to be done against the total electric field due to both the charges `q_(1)andq_(2)`. So the work done to bring the charge `q_(3)` is `=q_(3)(V_(1C)+V_(2C))`. Here `V_(1C)` is the electrostatic potential due to charge `q_(1)` at point C and `V_(2C)` is the electrostatic potential due to charge `q_(2)` at point C. The electrostatic potential is
`U=(1)/((4piepsi_(0)))((q_(1)q_(2))/(r_(13))+(q_(2)q_(3))/(r_(23)))" ".........(3)`
(d) Adding equations (2) and (3), the total electriostatic potential energy for the system of three charges `q_(1),q_(2)andq_(3)` is
`U=(1)/((4piepsi_(0)))((q_(1)q_(2))/(r_(12))+(q_(1)q_(3))/(r_(13))+(q_(2)q_(3))/(r_(23)))" ".......(4)`
stored potential energy U is equal to the total external work done to assemble the three charges at the givne locations.
