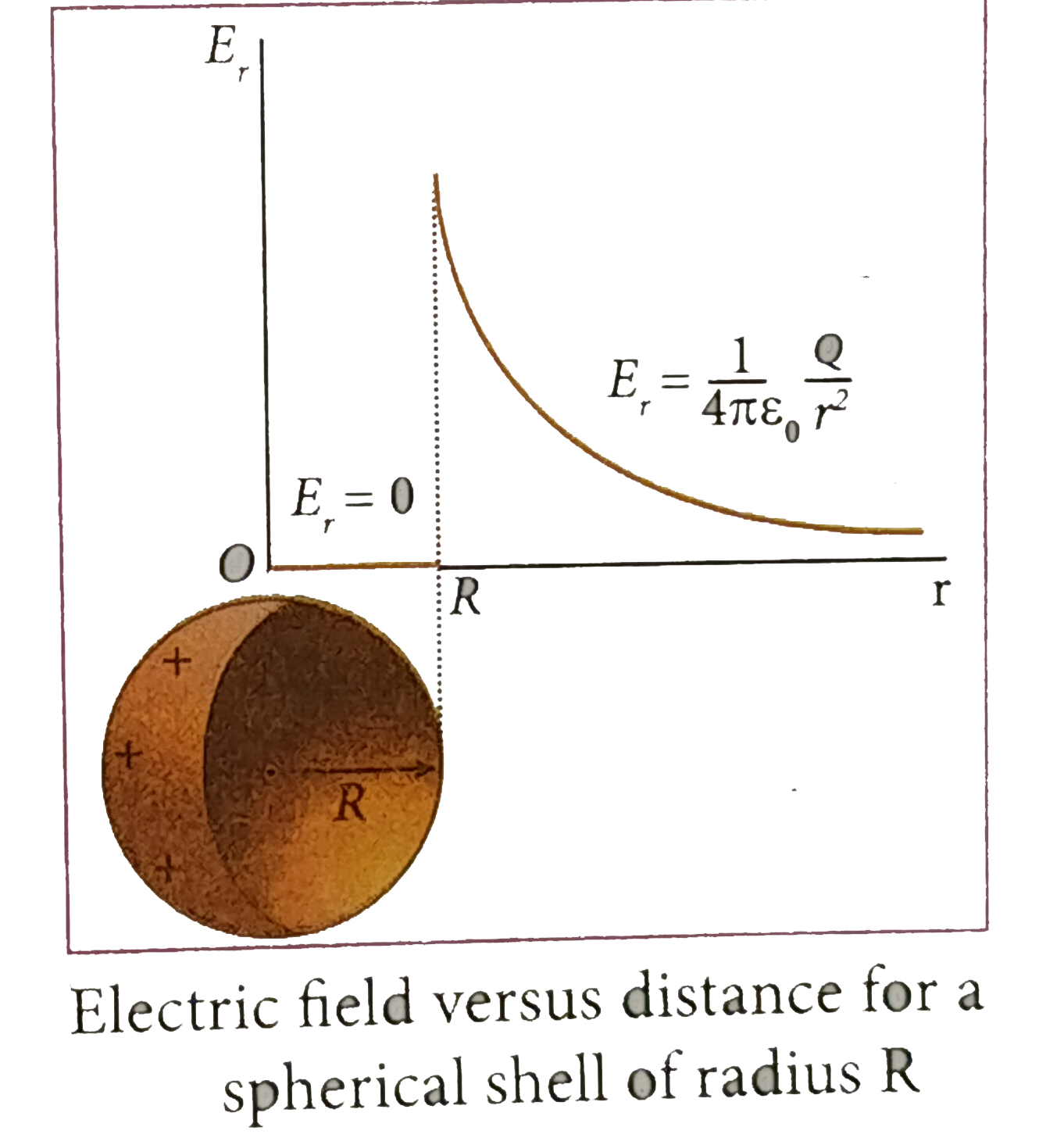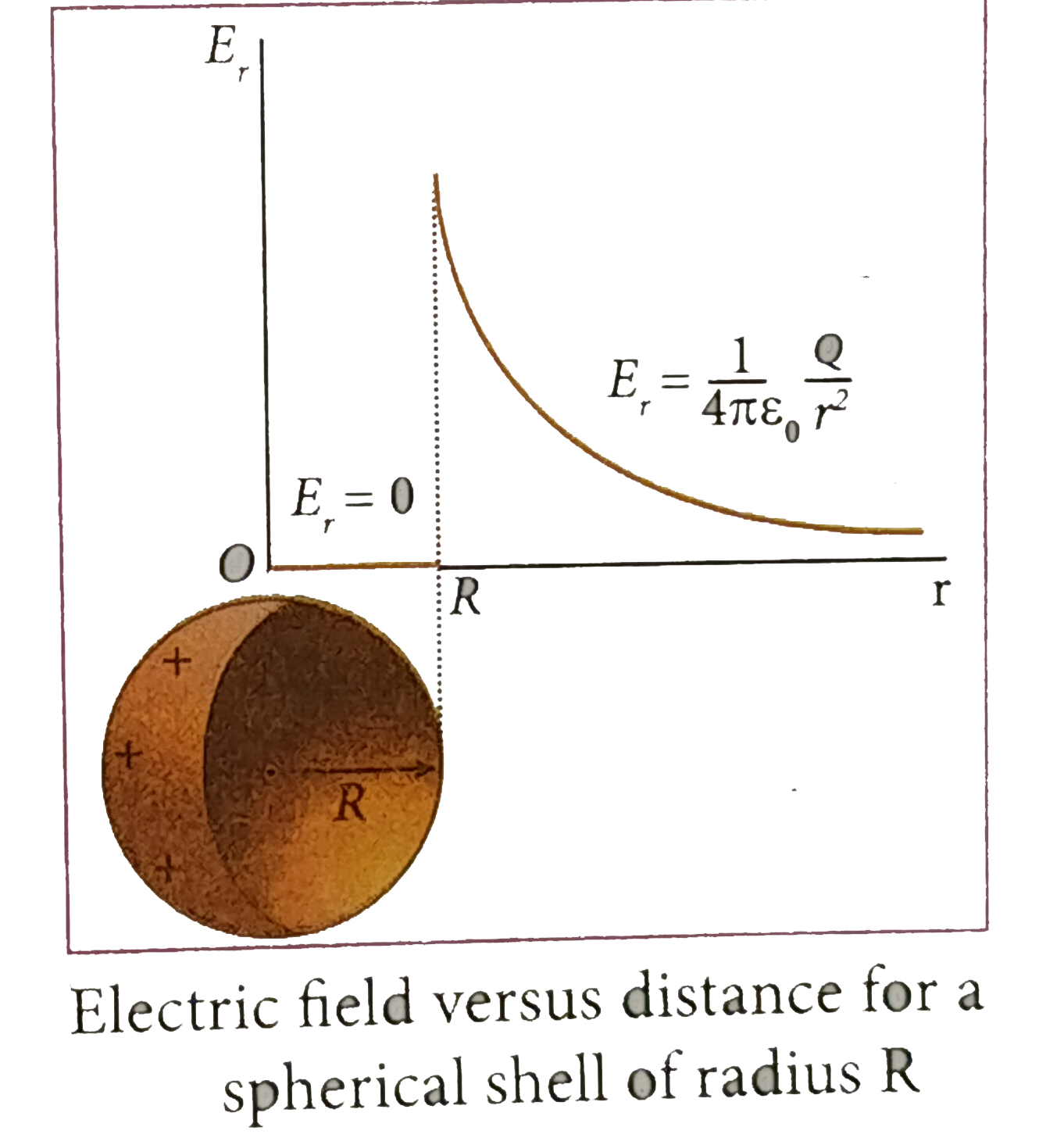Electric field due to a uniformly charged spherical shell :
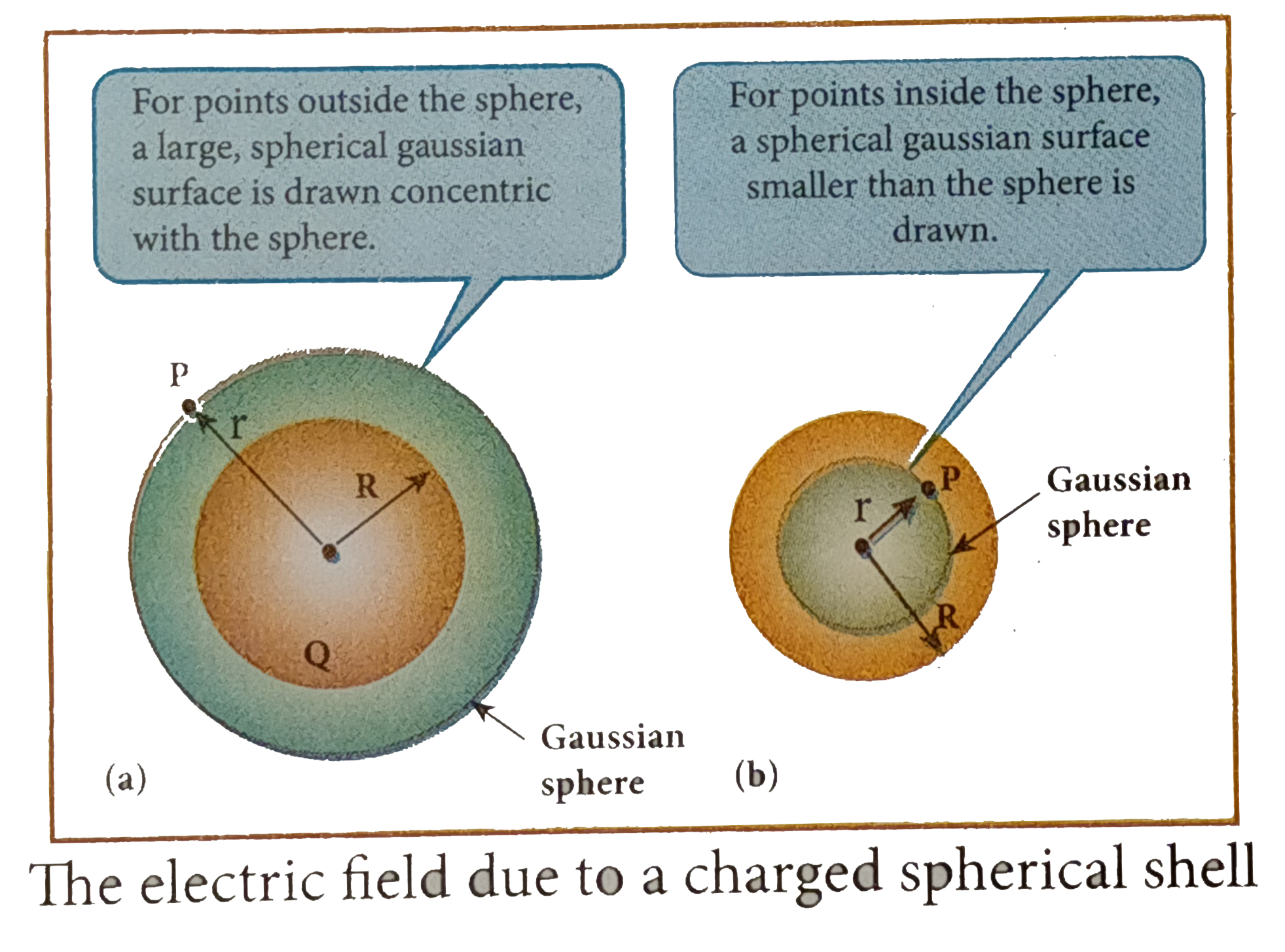
Consider a uniformly charged spherical shell of radius R and total charge Q as shown in Figure 1.42. The electric field at points outside and inside the sphere is found using Gauss law.
Case (a) At a point outside the shell `(rgtR)` (i) A point P outside the shell at a distance r from the center as shown in Figure (a). The charge is uniformly distributed on the surface of the sphere (spherical symmetry). Hence the electric field must point radially outward if `Qgt0` and point radially inward if `Qlt0`.
(ii) A spherical Gaussian surface of radius r is chosen and the total charge enclosed by this Gaussian surface is Q. Applying Gauss law
`underset("Gaussion surface")ointvecE.dvecA=(Q)/(epsi_(0))" ".........(1)`
(iii) The electric field `vec(E)anddvecA` point in the same direction (outward normal) at all the points on the Gaussian surface. The magnitude of `vec(E)` is also the same at all points due to the spherical symmetry of the charge distributtion
Hence `Eunderset("Gaussion surface")ointdA=(Q)/(epsi_(0))" ".......(2)`
But `underset("Curved surface")ointdA` total area of Gaussian surface surface `=4pir^(2)`. Substituting this in equation (2), `E.4pir^(2)=(Q)/(epsi_(0))`
`E.4pir^(2)=(Q)/(epsi_(0))(or)E=(1)/(4piepsi_(0))(Q)/(r^(2))`
In vector form `vec(E)=(1)/(4piepsi_(0))(Q)/(r^(2))hatr" "......(3)`
(iv) The electric field is radially outward if `Qgt0` and radially inward if `Qlt0`. Form equation (3), the electric field at a point outside the shell will be same as if the entire charge Q is concentrated at the center of the spherical shell.
Case (b): At a point on the surface of the shperical shell (r=R): The electrical field at points on the spherical shell (r=R) is given by
`vec(E)=(Q)/(4piepsi_(0)R^(2))hatr" "......(4)`
Case (c) At a point inside the spherical shell `(rltR)`: Consider a point P inside the shell at a distance r from the center. A Guassian sphere of radius r is constructed as shown in the Figure (b). Applying Gauss law
`underset("Gaussion suface")ointvec(E).dvecA=(Q)/(epsi_(0))`
`E.4pir^(2)=(Q)/(epsi_(0))" "......(5)`
Since Gaussian surface encloses no charge, So Q=0. The equation (5) becomes
`E=0" "(rltR)" ".......(6)`
The electric field due to the uniformly charged spherical shell is zero at all points inside the shell. A graph can be plotted between the electric field and radial distance. This is shown in Figure.