Case (i): Electric field due to an electric dipole at points on the axial line:
Consider an electric dipole placed on the x-axis. A point C is located at a distance of r from the midpoint O (of the diole) along the axial line.
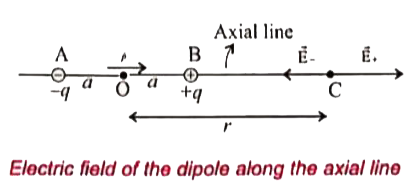
The electric field at a point C due to +q is
`vecE_+ = 1/(4piepsilon_0)q/((r-a)^2)` along BC.
Since the electric dipole moment vector `vecp` is from -q to +q and is directed along BC, the above equation is written as
`vecE_+ = 1/(4piepsilon_0)q/((r-a)^2)hatp`
where `hatp` is the electric dipole moment unit vector from -q to +q.
The electric field at a point C due to -q is
`vecE_- = 1/(4piepsilon_0)q/((r+a)^2)hatp`
Since +q is located closer to the point C than -q, `vecE_+` is stronger than `vecE_-`. Hence, the length of the `vecE_+` vector is drawn larger than that of `vecE_-` vector.
The total electric field at point C is calculated using the superposition principle of the electric feild.
`vecE_("tot") = vecE_+ + vecE_-`
`= 1/(4piepsilon_0)q/((r-a)^2)hatp - 1/(4piepsilon_0)q/((r+a)^2)hatp`
`vecE_("tot") = q/(4piepsilon_0)(1/((r-a)^2) - 1/((r+a)^2))hatp`
`vecE_("tot") = 1/(4piepsilon_0)q((4ra)/((r^2-a^2)^2))hatp` ...(1)
Note that the total electric field is along `vecE_+`, since +q is closer to C than -q.
If the point C is very far away from the dipole then `(r gt gt a)`. Using this limt the tern `(r^2-a^2)^2 approx r^4`. Subsituting this into equation (1), we get
`vecE_("tot") = 1/(4piepsilon_0)((4aq)/r^3)hatp` `(r gtgt a)`
since 2aq `hatp = vecP`
`vecE_("tot") = 1/(4piepsilon_0)(2vecp)/r^3` `(r gtgt a)`
The dierection of `vecE_("tot")` is shown in figure.

If the point C is selected on the left side of the dipole, the total electric field is still in te direction of `vecp`. This result is inferred by examining the electric field lines of the dipole.
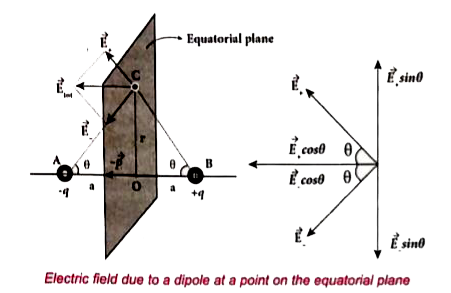
Case (ii): Electric field due to an electric dipole at a point on the equatorial plane:
Consider a pont C at a distance r from the midpoint O of the dipole on the equatorial plane.
Since the point C is equi-distant from +q and -q, the magnitude of the electric fields of +q and -q are the same. The direction of `vecE_+` is along BC and the direction `vecE_-` of is along CA. `vecE_+` and `vecE_-` are resolved into two components, one component parallel to the dipole axis and the other perpendicular components `|vecE_+| sintheta` and `|vecE_-| sintheta` are oppositely directed and cancel each other. The magnitude of the total electric field at the point C is the sum of the parallel compoents of `vecE_+` and `vecE_-` and its direction is along `-hatp` as shown in the figure.
`vecE_("tot") = -|vecE_+|costhetahatp-|vecE_=|costhetahatp` (2)
The magnitude `vecE_+` and `vecE_-` are the same and are given by
`|vecE_+| = |vecE_-| = 1/(4piepsilon_0)q/((r^2-a^2))` ...(3)
By subsituting equatoin (3) into equation (2), we get
`vecE_("tot") = -1/(4piepsilon_0)(2q costheta)/((r^2+a^2))hatp`
`= -1/(4piepsilon_0)(2q costheta)/((r^2+a^2)^(1/2))hatp`
since `costheta = a/(sqrt(r^2+a^2))`
`vecE_("tot") = -1/(4piepsilon_0)hatp/((r^2+a^2)^(1/2))`
since `vecp = 2aqahatp` ...(4)
At very alrge distances `(r gtgt a)`, the equation (4) becomes.