Let us consider two equal and opposite charges separated by a small distance 2a. Let the point P is located at a distance r from the midpoint of the dipole. Let 0 be the angle between the line OP and dipole axisa AB.
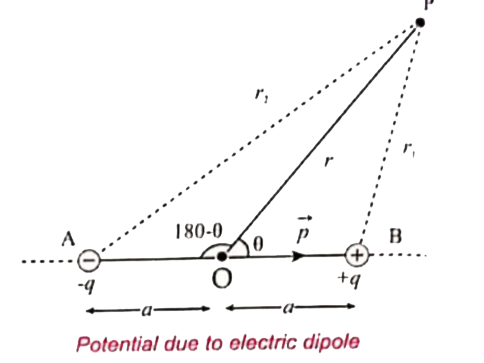
Let `r_1` be the distance of point P from +q and `r_2` be the distance of point P from -q.
Potential at P due to charge `+q = 1/(4piepsilon_0)q/r_1`
Potential at P due to charge `-q = 1/(4piepsilon_0)q/r_2`
Total potential at the point P,
`V= 1/(4piepsilon_0)q(1/r_1-1/r_2)` ---(1)
Suppose if the point P is far away from the dipole, such that `a ltlt r`, then equation (1) can be expressed in terms of r.
By the cosine law for triangle BOP,
`r_1 = r_2 + a^2 - 2racostheta`
`r_1^2 = r^2(1 + a^2/r^2 - (2a)/rcostheta)`
Since `a/r ltlt 1`, we can use binomial theorem and retain the terms up to first order,
`1/r_1 = 1/r(1+ a/rcostheta)` ...(2)
Similarly applying the cosine law for triangle AOP.
`r_2^2 = r^2 + a^2 - 2ra cos(180-0)`
Since,
`cos(180-theta) = -costheta ` we get
`r_2^2 = r^2 + a^2 + 2ra costheta`
Neglecting `a^2/r^2`
`r_2^2 = r^2(1+ (2acostheta)/r)`
`r_2 = r(1+ (2acostheta)/r)^(1/2)`
Using Binomial theorem, we get,
`1/r_2 = 1/r(1-(acostheta)/r)` ...(3)
Subsitiuing equation (2) and (3) in equation (1)
`V = 1/(4piepsilon_0)q[1/r(1+a(costheta)/r)-1/r(1-a(costheta)/r)]`
`V = q/(4piepsilon_0)[1/r(1+a(costheta)/r-1+a(costheta)/r)]`
`V = 1/(4piepsilon_0)(2aq)/r^2 costheta`
But the electric dipole moment p = 2qa and we get,
`V = 1/(4piepsilon_0)((pcostheta)/r^2)`
Now we can write `pcostheta = vecp.hatr`, where `hatr` is the unit vector from the point O to point P. Hence the electric potential at a point P due to an electric dipole is given by
`V = 1/(4piepsilon_0)(vecp.hatr)/r^2 :. (r gtgt a)` ...(4)
Equation (4) is valid for distances very large compared to the size of the dipole. But for a point dipole, the equation (4) is valid for any distance.
Special cases
Case (i): If the point P lies on the axial line pf the dipole on the side of +q, then `theta = 0`. Then the electric potential becomes
`V = 1/(4piepsilon_0)p/r^2`
Case (ii): If the point P lies on the axial line dipole on the side of -q, then `theta=180^@`, then
`V = -1/(4piepsilon_0)p/r^2`
Case (iii): If the point P lies on the equatorial line of the dipole, then `theta=90^@`.
Hence V = 0
