The electric potential at a point at a distance r from which point charge `q_1` is given by
`V = 1/(4piepsilon_0)q_1/r^2` …(1)
This potential V is the work done to bring a unit positive charge from infinity to the point. Now if the charge `q_2` is brought r rom `q_1`, the work done is the product of `q_2` and the electric potential at that point. Thus we have
`W = q_2V` ...(2)
This work done is stroed as the electrostatic potential energy U of a system charges `q_1` and `q_2` separated by a distance r. Thus we have
`U = q_2V = 1/(4piepsilon_0)(q_1q_2)/r` ...(3)
The electrostatic potential energy epends only the distance between the two point charges. In fact, the expression (3) is derived by assuming that `q_1` is ifxed and `q_2` is brought from infinity. The equation (3) holds true when `q_2` is fixed and `q_1` is brought from infinity or both `q_1` and `q_2` are simultaneously brought from infinity to a distance r between them.
Three charges are arranged in following configuration.
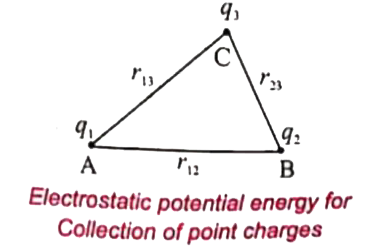
To calcualte the total electrostatic potential energy, the following procedureis used. Bring all the charges one by one and arrange them according to the configuration.
(i) Bringing a charge `q_1` from infinity to the point A requires no work, because there are no other charges already present in the vinicity of charge `q_1`.
(ii) To bring the second charge `q_2` to the point B, work must be done against the electric field at B created by the charge `q_2` is `q_1`. So the work done on the charge `q_2` is `W = q_2 V_(1B)`. Here `V_(1B)` is the electrostatic potential due to the charge `q_1` at point B.
`U = 1/(4piepsilon_0)(q_1q_2)/r_12`
It is noted that the expression is same when `q_2` is brought first and then `q_1` later.
(iii) In the same way, to bring the charge`q_3` to the point C, work has to be done against the total electric field due to both the charges `q_1` and `q_2`. So the work done to bring the charges `q_3` is `= q_3 (V_(1C) + V_(2C))`. Here `V_(1C)` is the electrostatic potential due to charge `q_1` at point C and `V_(2C)` is the electrostatic potential due to charge `q_2` at point C.
The electroststic potential is
`U = 1/(4piepsilon_0)((q_1q_3)/r_13+ (q_2q_3)/r_23)` ...(5)
(iv) Adding equations (4 and 5), the total electrostatic potential energy for the system of three charges `q_1,q_2` and `q_3` is
`U = 1/(4piepsilon_0)((q_1q_2)/r_12+ (q_1q_3)/r_13 + (q_2q_3)/r_23)` ...(6)
It is noticed that this stored potential energy U is equal to the total external work done to assemble the three charges at the given locations. The expression (6) is same even if the charges are brought to their positions in any other order. Since the Coulomb force is a conservative force, the electrostatic potential energy is independent of the manner in which the configuration of charges is arrived at.
