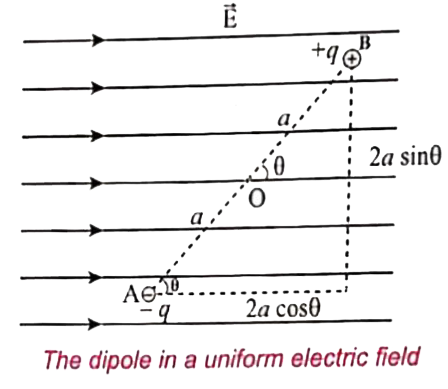
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Derive an expression for electrostatic potential energy of the dipole ...
Text Solution
|
- Potential Energy Of An Electric Dipole In A Uniform Electric Field
Text Solution
|
- Derive an expression for potential energy of an electric dipole in a u...
Text Solution
|
- Derive an expression for the potential energy of an electric dipole pl...
Text Solution
|
- Derive the expression for the potential energy of an electric dipole o...
Text Solution
|
- Derive an expression for potential energy of electric-dipole placed in...
Text Solution
|
- Derive an expression for electrostatic potential due to an electric di...
Text Solution
|
- Derive an expression for electrostatic potential due to an electric di...
Text Solution
|
- Derive an expression for electrostatic potential energy of the dipole ...
Text Solution
|