The various properties of conductors at electrostatic equilibrium are -
(i) The electric field is zero everywhere inside the conductor. This is true regardless of whether the conductor is solid or hollow.
This is an experimental fact. Suppose the electric field is not zero inside the metal, then there will be a force on the mobile charge carriers due to this electric field. Hence, there will be a net motion of the mobile charges, that contradicts being in electroststic equilibrium. Thus the electric field is zero everywhere inside the conductor.
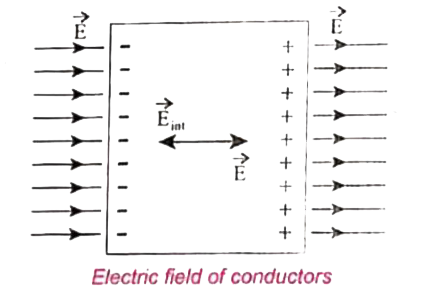
When an electric field is applied, the free electrons accelerate to the left causing the left plate to be negatively charged.
Due to this realignment of free electrons, there will be an internal electric field created inside the conductor which increases until it nullified the conductor is said to be in electrostatic equilibrium is inthe order to `10^(-16)`g, which can be taken as almost instantaneous.
(ii) There is no charge inside the conductors. The charge must reside only on the surface of the conductors.
Let us prove this property using Gauss law. Consider an arbitrarily shaped conductor.
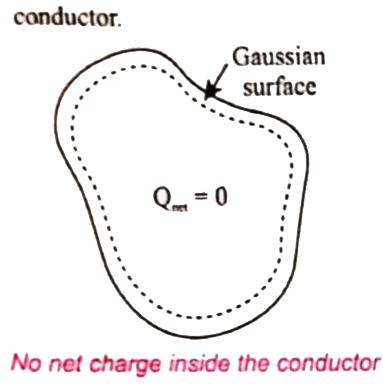
A Gaussian surface is drawn inside the conductor such that it is very close to the surface of the conductor. Since the electric field is zero over this Gaussian surface. From Gauss.s law, it is implied that there is no charge inside the conductor. Even if no net charge is introduced inside the conductor , it immediately reaches the surface of the conductor.
(iii) The electric field outside the conductor is perpendicular to the surface of the conductor and has a magnitude of `sigma/epsilon_0` where `sigma` is the surface charge density at that point.
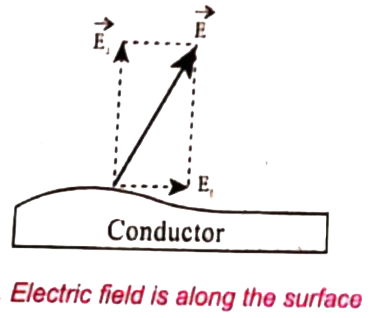

If the electric field has components parallel to the surface of the conductor, then free electrons on the surface of the conductor would experience acceleration (Fig (a)). It is meant that the electrostatic equilibrium, the electric field must be perpendicualr to the surface of the conductor (Fig (a)).
We know that the electric field has amgniyude `sigma/epsilon_0` just outside the conductor.s surface. Consider a small cylindrical Gassian surface, as shown in the figure. One half of this cylinder is embedded inside the conductor.
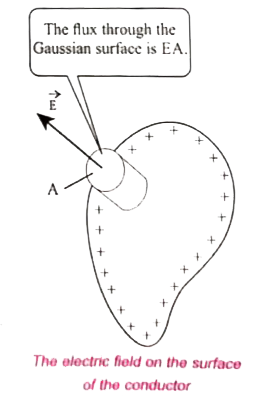
Since electric field is normal to the surface of the conductor, the curve part of the cylinder has zero electric flux. Also inside the conductor, the electric field is zero. Hence the bottom flat part of the Gaussian surface has no electric flux.
Hence the top flat surface alone contributes to the electric flux. The electric field is parallel to the area vector and the total charge inside the surface is `sigmaA`. By applying Gauss.s law,
`EA = (sigmaA)/epsilon_0`
In vector form,
`vecE = sigma/epsilon_0hatn`
Here `hatn` represents the unit vector outward normal to the surface of the conductor `sigma lt o`, then electric field points inward perpendicular to the surface.
(iv) The electrostatic potential has the same value on the surface and inside of the conductor.
We know that the conductor has no parallel electric component on the surface without doing any work. This is possible only if the electrostatic potential difference between any two points on the surface. Since the electric field is zero inside the conductor. Thus at electrostatic equilibrium, the conductor is always at equipotential.




