(i) Capacitors in series:
Consider three cpacitors of capacitance `C_1,C_2` and `C_3` connected in series with a battery of ovltage V as shown in the Figure (a).

As soon as the battery connected to the capacitors in series, the electrons of charge - Q are transferred from negative terminal to the right plate of `C_3` which pushes the electrons of same amount - Q from left plate of `C_3` to the right plate of `C_2` due to electrostatic induction. Similarly, the left plate of `C_2` pushes the charge of - Q to the right plate of `C_1` that induces the positive charge +Q on the left plate of `C_1`. At the same time, electrons of charge - Q are transferred from left plate of `C_1` to positive terminal of the battery.
By these processes, each capacitor stores the same amount of charge Q. The caacitances of the capacitors are in general different, so that the voltage across each different, so that the volatge across each capacitor is also different and are denoted as `V_1,V_2` and `V_3` respewctively.
The total voltage across each capacitor must be equal to the voltage of the battery.
`V = V_1 + V_2 + V_3`
Since Q = CV, we have
`V = Q/C_1+Q/C_2+Q/C_3`
`= Q(1/C_1+1/C_2+1/C_3)`
If three capacitors in series are considered to form an equivalent single capacitor C. (Fig. (b)), then we have `V = Q/C_S` Substituting this expression into equation we get
`Q/C_S = Q(1/C_1+1/C_2+1/C_3)`
`1/C_S = 1/C_1+1/C_2+1/C_3`
Thus, the inverse of the equivalent capacitance `C_S` of three capacitors connected in series is equal to the sum of the inverse of each capacitance. This equivalent capacitance `C_S` is always less than the smallest individual capacitance in the series.
(ii) Capacitance in parallel:
Let us concider three capacitors of capacitance `C_1,C_2` and `C_3` connected in parallel with a battery of volatge V (Fig.(a))
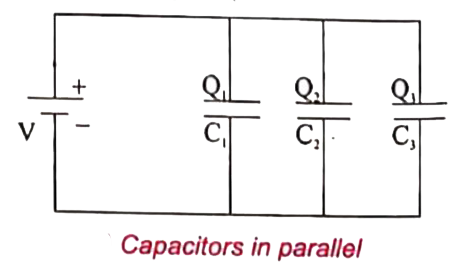

Since corresponding sides of the capacitors are connected to the same positive and negative terminals of the battery, the voltage across each capacitor is equal to the battery.s voltage. Since capacitance of the capacitors is different, the charge stored in each capacitor is not the same. Let the charge stored in the three capacitors be `Q_1,Q_2` and `Q_3` respectively. According to the law of conservation of total charges, the sum of these three charges equal to the charge Q transferred by the battery.
`Q = Q_1+Q_2+Q_3`
Now, since Q = CV, we have
`Q = C_1V+C_2V+C_3V`
If these three capacitors are considered to form a single capacitance `C_P` which stores the toal charge Q as shown in the Figure (b), then we can write `Q = C_PV`.
Substituting this in above equation, we get `C_PV = C_1V+C_2V+C_3V`
`C_P = C_1+C_2+C_3`
Thus, the equivalent capacitance of capacitors connected is always gretaer than the largest individual capacitance. In a parallel connection, it is equivalent as area of each capacitance adds to give more effective area such that capacitance increases.


