Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
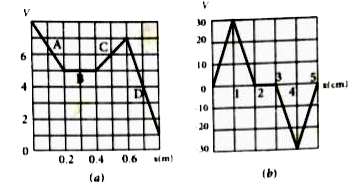
- The electrostatic potential is given as a function of x in figure ( a)...
Text Solution
|
- Figure shows a plot of the conservative force F in a unidimensional fi...
Text Solution
|
- A graph of the x-component of the electric field as a function of x in...
Text Solution
|
- A, B and C are three points in an electrostatics field. The electric p...
Text Solution
|
- The figure gives the electric potential V as a function of distance th...
Text Solution
|
- The following figure represents the electric potential as a function o...
Text Solution
|
- The electrostatic potential is given as a function of x in figure ( a)...
Text Solution
|
- The electric potential as a function of distance 'x' is shown in the f...
Text Solution
|
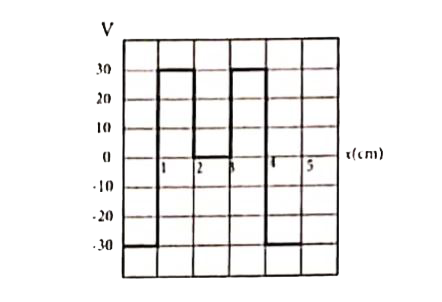
- A V - X graph for an electric field in X-direction is shown in the fig...
Text Solution
|