Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
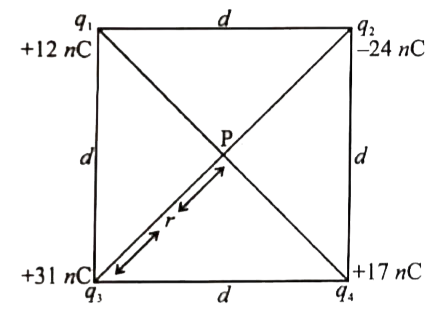
- A square of side 1.3 m has charges +12 nC, -24nC, +31nC and +17nC at i...
Text Solution
|
- Four spheres, each of diameter 2a and mass M are placed with their cen...
Text Solution
|
- Three charges ,each of + 4 mu C ,are placed at the corners A,B,C of a ...
Text Solution
|
- A charge of 60n C (nanocouloumb) is palced at the corner A of a square...
Text Solution
|
- Electric charges of +10 muC,+5 muC,-3 muC and +8 muC are placed at the...
Text Solution
|
- Four point charges are placed at the corners of a square of side l. Ca...
Text Solution
|
- भुजा a वाले एक वर्ग के प्रत्येक कोने पर आवेश q रखा है। वर्ग के केन्द्र...
Text Solution
|
- Find the electric field and potential at the centre of a square of sid...
Text Solution
|
- Four point charges of +1muc each are placed on the four corners of a s...
Text Solution
|