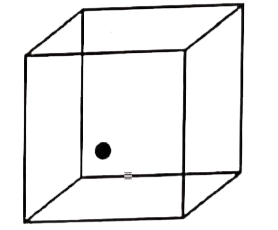
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the electric flux through each face of a hollow cube of side 10 c...
Text Solution
|
- A cube of side 10 cm encloses a charge of 0.1 muC at its center. Calcu...
Text Solution
|
- A charge q is placed at the centre of a cube of side l what is the el...
Text Solution
|
- A charge q muC is placed at the centre of a cube of a side 0.1m, then ...
Text Solution
|
- Find the electric flux through each face of a hollow cube of side 10 c...
Text Solution
|
- A charge of q muC is placed at the centre of a cube of side 0.1 m. the...
Text Solution
|
- A point charge of 12muC is placed at the centre of a cube of side 1m. ...
Text Solution
|
- An electric charge q is placed at the centre of a cube of side l. The ...
Text Solution
|
- A charge q is placed at the centre of a cube of side l what is the ele...
Text Solution
|