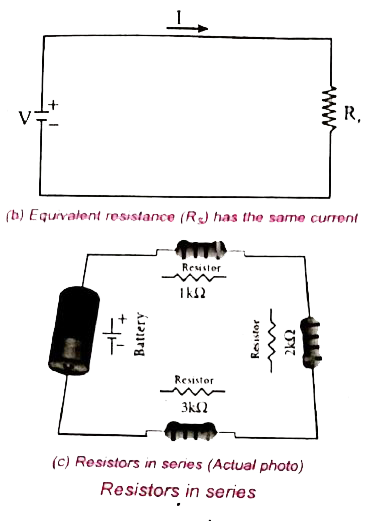
When two or more resistors are connected end to end, they are said to be in series. Three resistors `R_1, R_2` and `R_3` connected in series. (Fig. (a)).
The number of charges passing through resistor Rį must also pass through resistors `R_2` and `R_3` since the charges cannot accumulate anywhere in the circuit. Here the current I passing through all the three resistors are the same. According to Ohm.s law, if same current pass through different resistors of different values, then the potential difference across each resistor must be different. Let `V_1, V_2` and `V_3` be the potential difference (voltage) across each of the resistors `R_1, R_2` and `R_3` respectively, then we can write `V_1 = IR_1, V_2 = IR_2` and `V_3 = IR_3`. But the total voltage V is equal to the sum of voltages across each resistor.
`V = V_1 + V_2 + V_3`
` = IR_1 +IR_2 + IR_3" ...(1)"`
` V = I (R_1 + R_2 + R_3)`
` V = I.R_s" ...(2)"`
Where `R_S` is the equivalent resistance,
` R_S = R_1 + R_2 + R_3" ...(3)"`
When several resistances are connected in series, the total or equivalent resistance is the sum of the individual resistances. (Fig. (b)).
Resistors in parallel: When resistors are connected across the same potential difference. They are in parallel.
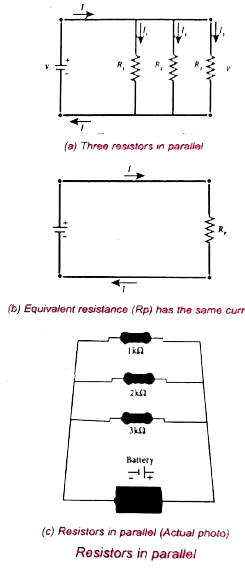
In this case, the total current I that leave the battery split into three separate paths. Let `I_1, I_2` and `I_3` be the current through the resistors `R_1, R_2` and `R_3`, respectively. Due to the conservation of charge, total current in the circuit I is equal to sum of the currents through each of the three resistors,
`I = I_1 + I_2 +I_3" ...(4)"`
Since the voltage across each resistor is the same. According to Ohm.s law to each resistor, we get
`I_1 = V/R_1 , I_2 = V/R_2 , I_3 = V/R_3 " ...(5)"`
Substituting these values in equation (4), we get
`I = V/R_1 + V/R_2 + V/R_3`
`=V [1/R_1 + 1/R_2 + 1/R_3]`
` I = V/R_p`
` 1/R_p = 1/R_1 + 1/R_Z+ 1/R_3" ...(6) "`
Here `R_p` is the equivalent resistance of the parallel combination of the resistors. Thus, when a number of resistors are connected in parallel, the sum of the reciprocal of the values of resistance of the individual resistor is equal to the reciprocal of the effective resistance of the combination.(Fig. (b))
The value of equivalent resistance in parallel connection will be lesser than each individual resistance.