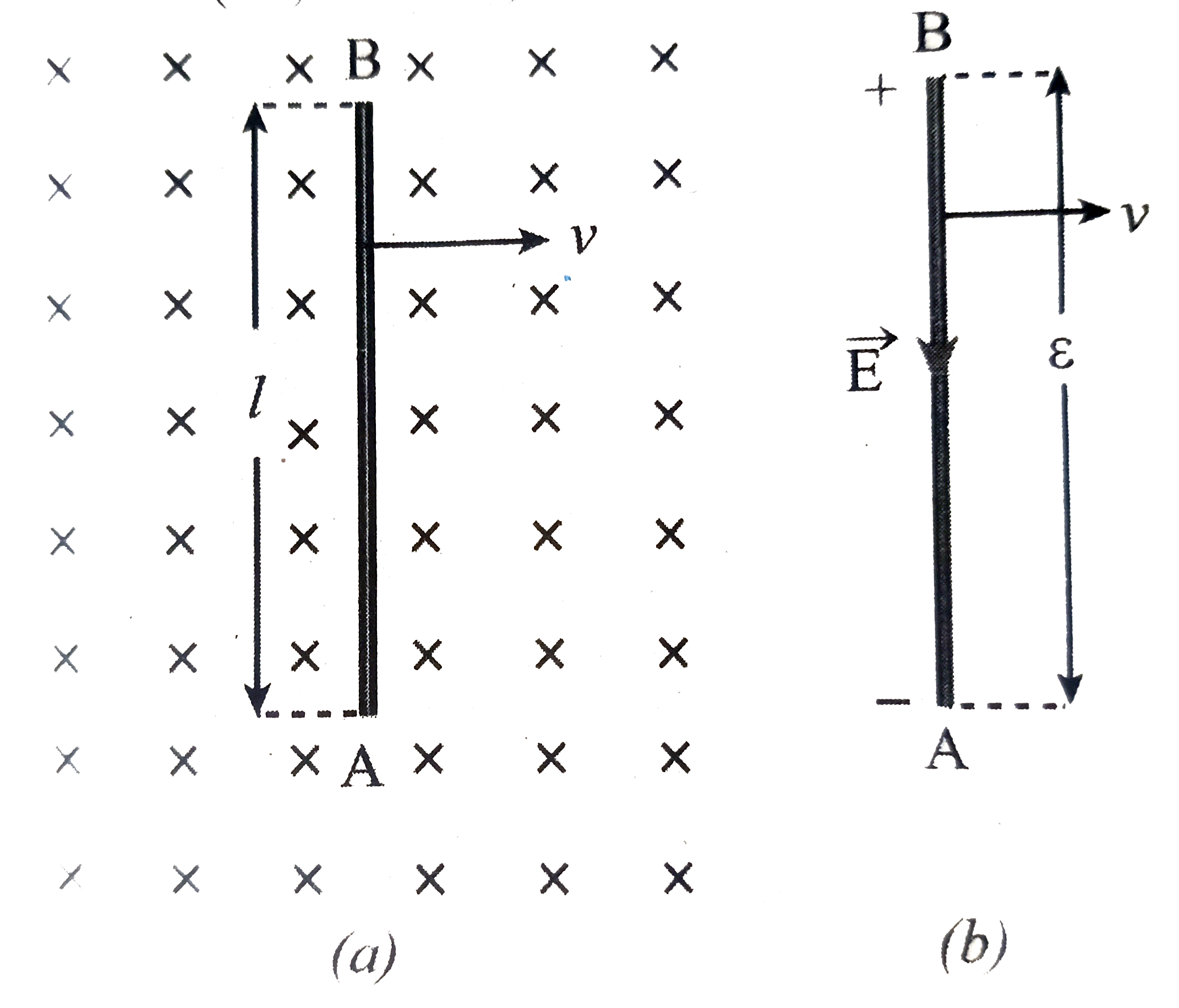Let us consider a straight conducting rod AB of length l in a uniform magnetic field `vecB` which is directed prependicularly into the plane of the paper (fig (a)). The length of the rod is normal to the magnetic field. Let the rod move with a constant velocity `vecv` towards right side.
When the rod moves, the free electrons present in it also move with same velocity `vecv`in `vecB`. As a result, the Lorentz force acts on free electrons in the direction from B to A and given by the realtion.
`vecF_(B)=-e(vecvtimesvecB)` ...(1) ,br> The actoin of this Lorentz force is to accumulate the free electrons at the end A. This accumulation of free electrons produces a potential difference across the rod which in turn established an electric field `vecE` directed along BA (fig (b)). Due to the electric field `vecE`, the coulomb force starts acting on the free electrons along AB and is given by
`vecF_(E)=-evecE` ...(2)
The magnitude of the electric field `vecE` keeps on increasing as long as accumulation of electrons at end a continues. The force `vecF_(E)` also increases until equilibrium is reached. At equilibrium, the megnetic Lorentz force `vecF_(B)` and the coulomb force `vecF_(E)` balance each other. Hence no further accumultion of free electrons at the end A takes place.
i.e, `|vecF_(B)|=|vecF_(E)|`
`|-e(vecvtimesvecB)|=|-evecE|`
`vB sin 90^(@)=E`
vB=E
The potential difference between to ends of the rod is
V=El ...(3)
V=vBl
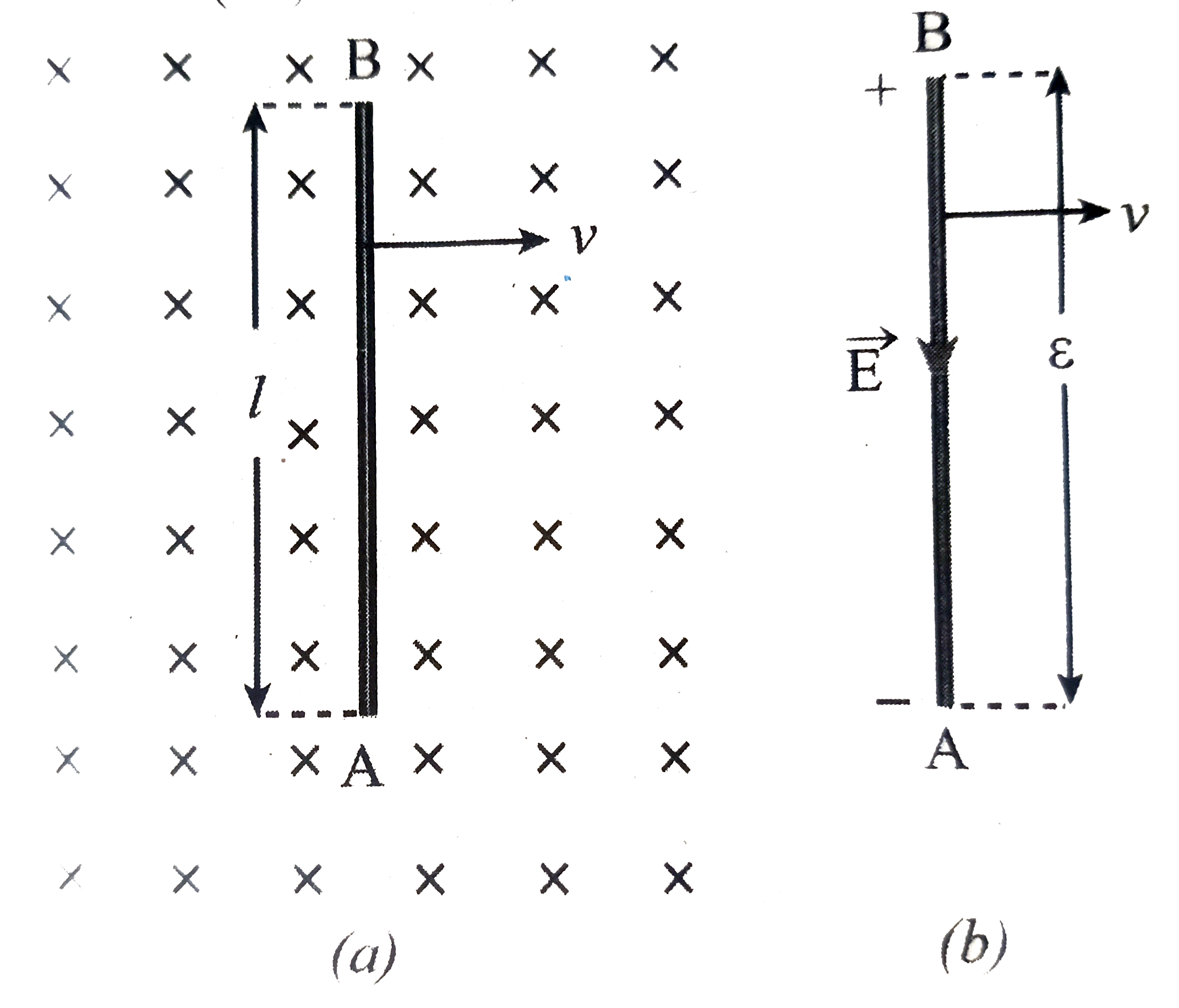
Thus the Lorentz force on the free electrons is responsible to maintain this potential difference and hence produces an emf
e=Blv ...(4)
As this emf is produced due to the movement of the rod, it is often called as motional emf. If the ends A and B are connected by an external circuit of total resistance R, then current `i=e/R=(Blv)/R` flows in it. The direction of the current is found from right - hand thumb rule.