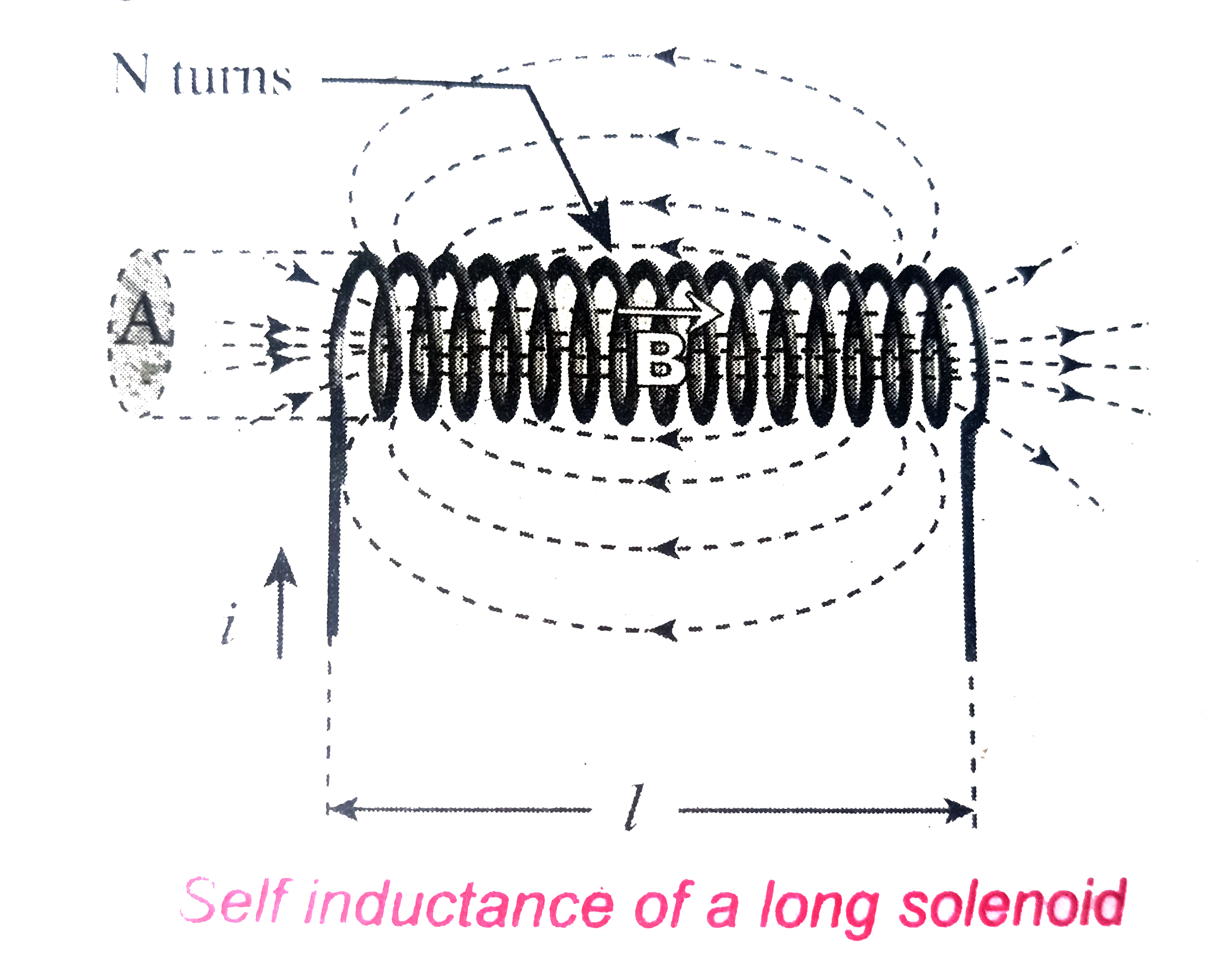
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Assuming that the length the of the solenoid is large when compared to...
Text Solution
|
- Consider the self-inductance per unit length of a solenoid at its cen...
Text Solution
|
- A solenoid of length l metre has self-inductance L henry. If number of...
Text Solution
|
- Find the inductance of a solenoid of length l whose winding is ma...
Text Solution
|
- The magnetic flux near the axis inside a current-carrying air-core sol...
Text Solution
|
- The self-inductance of a long straight solenoid is L. Each of the leng...
Text Solution
|
- The self-inductance of a solenoid is L. If it is compressed to half it...
Text Solution
|
- Assuming that the length the of the solenoid is large when compared to...
Text Solution
|
- For a solenoid keeping the turn density constant its length makes halv...
Text Solution
|