Let us consider two coils which are placed close to each other. If an electric current`i_(1)`is sent through coil 1, the magnetic field produced by it is also linked with coil 2 (fig (a)).
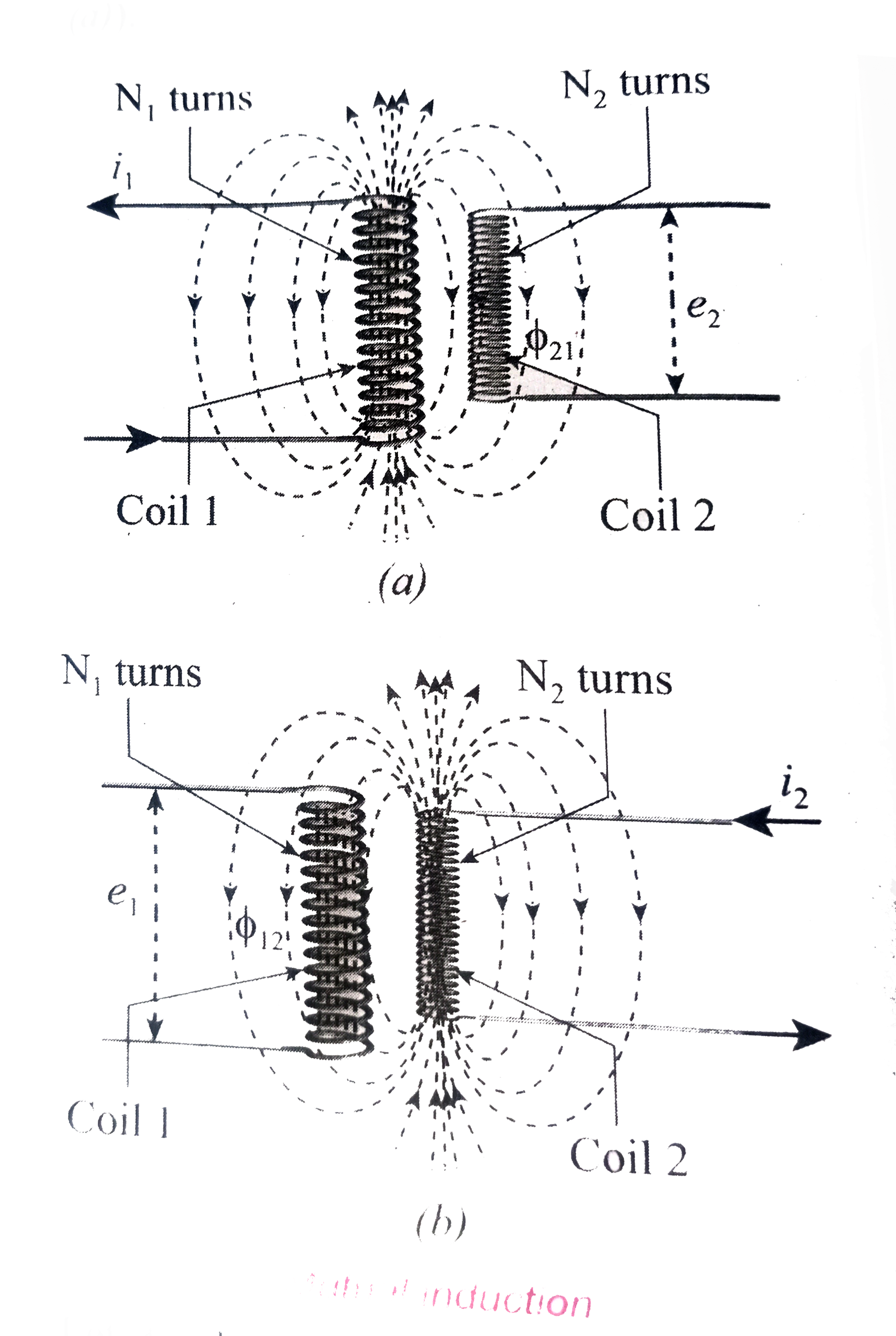
Let `phi_(21)` be the magnetic flux linked with each turn of the coil 2 of `N_(2)` turns due to coil 1, then the total flux linked with coil 2 `(N_(2)phi_(21))` is proportinal to the current `i_(1)` in the coil 1.
`N_(2)phi_(21)proptoi_(1)`
`N_(2)phi_(21)=M_(21)i_(1)" "...(1)`
(or) `M_(21)=(N_(2)phi_(21))/i_(1)`
The constant of proportionality `M_(21)` is the mutual inductance of the coil 2 with respect to coil 1. It is also called as coefficient of mutual induction . If `i_(1)=1A`, then
`M_(21)=N_(2)phi_(21)`
Therfeore, the mutual inductance `M_(21)` is defined as the flux linkage of the coil 2 when 1 A current flows through coil 1.
When the current `i_(1)` changes with time, an emf `e_(2)`is induced in coil 2. From Faraday.s law of electromagnetic induction. this mutually induced emf `e_(2)` is given by
`e_(2)=-(d(N_(2)phi_(21)))/(dt)=-(d(M_(21)i_(1)))/(dt)`
`e_(2)=-M_(21)(di_(1))/(dt)`
(or) `M_(21)=(-e_(2))/((di_(1))/(dt))`
The nagative sigh in the above equation shows that the mutually induced emf always opposes the change in current `i_(1)` with respect to time. If `(di_(1))/(dt)=1A_(S^(-1)),then" "M_(21)=-e_(2)`.
Mutual inductance `M_(21)` is also defined as the opposing emf induced in the coil 2 when the rate of change of current through the coil 1 is `1A_(S^(-1))`.
Similarly, if an electric current `i_(2)` through coil 2 changes with time, then emf `e_(1)` is induced in coil 1. Therefore,
`M_(12)=(N_(i)phi_(12))/(i_(2))" " and M_(12)=(-e_(1))/((di_(2))/dt)`
where `M_(12)` is the mutual inductance of the coil 1 with respect to coil 2. It can be shown that for a given pair of coils the mutual inductance is same.
i.e, `M_(21)=M_(12)=M`
