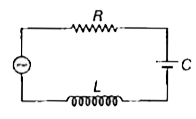
The differential equation of the emf for the circuit is
`L(dI)/(dt)+RI+(q)/(C)=v`
`=v_(m)sinomegat`
We know, that , I = dq / dt.
Therefore, di/dt = `d^(2)q/dt^(2)`. Thus in terms of q, the voltage equation becomes
`L(d^(2)q)/(dt^(2))+R(dq)/(dt)+(q)/(C)=v_(m)sinomegat " " ...(i)`
This is like he equation for a forced, damped oscillators.
Let us assume a solution
`q = q_(m) (omega t + theta)`
so that `(dq)/(dt) = q_(m) cos (omega t + theta)`
and `(d^(2)q)/(dt^(2)) - q_(m)omega^(2) sin(omega t + theta)`
On substituting these values in Eq. (i) we get
`q_(m)omega=[Rcos(omegat+theta)+(X_(C)-X_(L))`
`sin(omega+theta)=v_(m)sinomegat " " ...(ii)`
where we have used the relation `X_(C ) = 1 // omega C,`
`X_(L) = omega L`. Multiplying and dividing Eq. (ii)by
`Z=sqrt(R^(2)+(X_(C)-X_(L))^(2)),`
we have,
`q_(m)omegaz[(R)/(Z)cos(omegat+theta)+((X_(C)-X_(L)))/(Z)sin(omegat+theta)]`
`= V_(m) sin omega t`
Now, Let `" " (R )/(Z) = cos phi`
and `((X_(C)-X_(L)))/(Z)=sinphi`
So, that `" " phi = tan^(-1) (X_(C ) - X_(L))/(R )`
Substiltuting this in Eq. (ii) and simplifying we get
`q_(m)omegaZcos(omegat+theta-phi)=v-(m)sinomgat`
Comparing the two sides of this equation, we see that
`v_(m)=q_(m)omegaZ=i_(m)Z`
where
`i_(m) = q_(m)omega`
and `theta 0 phi = - (pi)/(2)`
or `theta = - (pi)/(2) + phi`
Therefore, the current in the circuit is
`i=(dq)/(dt)=q_(m)omegacos(omegat+theta)`
`=i_(m)cos(omegat+theta)`
or `i=i_(m)sin(omegat+phi)`
where `" " i_(m)=(V_(m))/(Z)=(V_(m))/(sqrt(R^(2)+(X_(C)-X_(L))^(2)))`
and `" " phi = tan^(-1) (X_(C) - X_(L))/(R )`
Clearly, `Z=sqrt(R^(2)+(X_(C)-X_(L))^(2))` is the effective resistane of the series L-C-R circuit which opposes or impedes the flow of current though it and is called its impedance.
Its SI units is ohm `(Omega)`.
Quality factor The Q-factor of a series resonant circuit is defined as the ratio of the resonant frequency to the difference in two frequencies taken on both sides of the resonant frequency such that at each frequency, the current amplutude becomes `(1)/(sqrt(2))` times the value at resonant frequency.
Mathematically, the Q-factor can be expressed as
`Q=(omega_(r))/(omega_(2)-omega_(1))=(omega_(r))/(2Deltaomega)=("resonant frequency")/("bandwidth")`
where `omega_(1) and omega_(2)` are the frequencies at which the current falls to `(1)/(sqrt(2))` times its resonant value.
