Consider all possible isomeric ketones, including stereoisomers of MW = 100. All these isomers are independently reacted with `NaBH_4` (Stereoisomers are also reacted seperately). The total number of ketones that give a racemic product(s) is…......
Consider all possible isomeric ketones, including stereoisomers of MW = 100. All these isomers are independently reacted with `NaBH_4` (Stereoisomers are also reacted seperately). The total number of ketones that give a racemic product(s) is…......
A
4
B
5
C
6
D
3
Text Solution
Verified by Experts
The correct Answer is:
5
The possible ketones with mol.wt.100 (`C_6H_(12)O`) are as follows. Out of these, the total number of ketones that give a racemic product(s) is 5. Their structure are:
`CH_3 -CH_2-CH_2-CH_2-overset(O)overset(||)C -CH_3 , CH_3-CH_2 -CH_2- overset(O)overset(||)C-CH_2-CH_3` ,
`CH_3 -underset(CH_3)underset(|)overset(CH_3)overset(|)C -overset(O)overset(||)C-CH_3, CH_3 overset(CH_3)overset(|"*")(CH)-COCH_2CH_3, CH_3 -overset("*")CH(CH_3) CH_2COCH_3`
Following ketone does not give racemic product.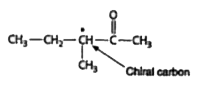
`CH_3 -CH_2-CH_2-CH_2-overset(O)overset(||)C -CH_3 , CH_3-CH_2 -CH_2- overset(O)overset(||)C-CH_2-CH_3` ,
`CH_3 -underset(CH_3)underset(|)overset(CH_3)overset(|)C -overset(O)overset(||)C-CH_3, CH_3 overset(CH_3)overset(|"*")(CH)-COCH_2CH_3, CH_3 -overset("*")CH(CH_3) CH_2COCH_3`
Following ketone does not give racemic product.

Similar Questions
Explore conceptually related problems
The noble gases have closed-shell electronic configuration and are monoatomic gases under normal conditions. The low boiling points of the lighter noble gases are due to the weak dispersion forces between the atoms and the absence of other interatomic interactions, The direct reaction of xenon with fluorine leads to a series of compounds with oxidation numbers +2, 4 and +6, XeF_4 reacts violently with water to give XeO_3 . The compouds of xenon exhibit rich stereochemistry and their geometries can be deduced considering the total number of electron pairs in the valence shell. Argon is used in arc welding because of its
Consider the number 2751. The sum of its digital is 2+7+5+1=15 . Adding the digits of 15 we get 1+5=6 . This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit) Let us see one more example. The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29 . Sum of digits of 29=2+9=11 . Sum of digits of 11=1+1=2 . Therefore the digital root of 679412 is 2 . Digital roots have an interesting property. To see this, consider the product 43times27=1161 . The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9 . Product of the digital roots= 7times9=63 . Digital root of 63=6+3=9 . The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=The digital root of 63 , where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers. The digital root of the number 63square5 is 8 (square represents a missing digit). Find the missing digit.
Consider the number 2751. The sum of its digital is 2+7+5+1=15 . Adding the digits of 15 we get 1+5=6 . This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit) Let us see one more example. The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29 . Sum of digits of 29=2+9=11 . Sum of digits of 11=1+1=2 . Therefore the digital root of 679412 is 2 . Digital roots have an interesting property. To see this, consider the product 43times27=1161 . The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9 . Product of the digital roots= 7times9=63 . Digital root of 63=6+3=9 . The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=The digital root of 63 , where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers. What is the digital root of 345?
Consider the number 2751. The sum of its digital is 2+7+5+1=15 . Adding the digits of 15 we get 1+5=6 . This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit) Let us see one more example. The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29 . Sum of digits of 29=2+9=11 . Sum of digits of 11=1+1=2 . Therefore the digital root of 679412 is 2 . Digital roots have an interesting property. To see this, consider the product 43times27=1161 . The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9 . Product of the digital roots= 7times9=63 . Digital root of 63=6+3=9 . The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=The digital root of 63 , where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers. What is the digital root of 927?
Consider the number 2751. The sum of its digital is 2+7+5+1=15 . Adding the digits of 15 we get 1+5=6 . This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit) Let us see one more example. The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29 . Sum of digits of 29=2+9=11 . Sum of digits of 11=1+1=2 . Therefore the digital root of 679412 is 2 . Digital roots have an interesting property. To see this, consider the product 43times27=1161 . The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9 . Product of the digital roots= 7times9=63 . Digital root of 63=6+3=9 . The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161 =The digital root of 63 , where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers. What is the digital root of 345times927 ?
Consider the number 2751. The sum of its digital is 2+7+5+1=15 . Adding the digits of 15 we get 1+5=6 . This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit) Let us see one more example. The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29 . Sum of digits of 29=2+9=11 . Sum of digits of 11=1+1=2 . Therefore the digital root of 679412 is 2 . Digital roots have an interesting property. To see this, consider the product 43times27=1161 . The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9 . Product of the digital roots= 7times9=63 . Digital root of 63=6+3=9 . The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161 =The digital root of 63 , where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers. If the digital root of a is 5 and the digital root of b is 2. Then what is the digital root of ab ?
Consider the number 2751. The sum of its digital is 2+7+5+1=15 . Adding the digits of 15 we get 1+5=6 . This number 6 is called the 'digital root' of the number 2751. That is, to find the digital root of a number, find the sum of its digits (Don't forget to find the sum of the digits again, if the first sum has more than one digit) Let us see one more example. The sum of the digits of the numbe 679412 is 6+7+9+4+1+2=29 . Sum of digits of 29=2+9=11 . Sum of digits of 11=1+1=2 . Therefore the digital root of 679412 is 2 . Digital roots have an interesting property. To see this, consider the product 43times27=1161 . The digital roots of the numbers 43 and 27 are 4+3=7 and 2+7=9 . Product of the digital roots= 7times9=63 . Digital root of 63=6+3=9 . The Digital root of 1161 is also 9(1+1+6+1=9) that is the digital root of 1161=The digital root of 63, where 63 is the product of the digital roots of 43 and 27. This property is true for all other natural numbers. 121times92=11square32 . Find the missing digit.
Primary alkyl halide C_4 H_9 Br (a) reacted with alcoholic K O H to give compound (b). Compound (b) is reacted with HBr to give (c) which is an isomer of (a). When (a) is reacted with sodtum metal it gives compound (d), C_ 8 H_ 18 which, is different from the compound formed when n-butyl bromide is reacted with sodium. Give the structural formula of (a) and write the equations for all the reactions.
Paragraph An organic compound A(C_(9)H_(6)O_(3)) does not react with aqueous solution of NaHCO_(3) as well as does not change the colour of litmus paper. Aon acid hydrolysis gives B(C_(9) H_(8)O_(4)) as major product whereas A on treatment with one equivalent of methanol in acidic medium gives C(C_(10)H_(10)O_(4)) as the major product (other minor isomer of C is also formed). B on heating with sodalime gives toluene. Answer the following questions based on the above information. The structure of product C is
Recommended Questions
- Consider all possible isomeric ketones, including stereoisomers of MW ...
Text Solution
|
- Consider all possible isomeric ketons including stereoisomers of MW =1...
Text Solution
|
- Consider all possible isomeric ketones including stereoisomers of rela...
Text Solution
|
- The maximum number of isomers (including stereoisomers ) that are poss...
Text Solution
|
- The maximum number of isomers (including stereoisomers) that are possi...
Text Solution
|
- Without considering stereoisomers the number of possible dibromobutane...
Text Solution
|
- सभी ऐल्डिहाइड्स तथा सभी कीटोन्स हैलोफॉर्म अभिक्रिया देते हैं।
Text Solution
|
- Consider all possible isomeric ketones, including stereoisomers of MW=...
Text Solution
|
- Give the total number of isomers including stereoisomers obtained on m...
Text Solution
|