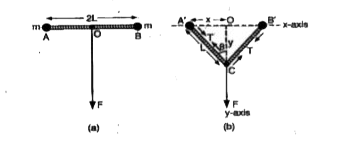
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two particles, each of mass m, are connected by a light string of len...
Text Solution
|
- An object of mass m is tied to a string of length l and a variable for...
Text Solution
|
- Two blocks of masses m and M are placed on a horizontal frictionless t...
Text Solution
|
- Two particles each of mass m are connected by a light string of length...
Text Solution
|
- Check the accuracy of the equation n = (1)/(2l)sqrt((F)/(m)) where...
Text Solution
|
- Two particles, each of mass m, are connected by a light string of leng...
Text Solution
|
- A string of length L and mass M is lying on a horizontal table. A forc...
Text Solution
|
- Two blocks of masses M and 2M are connected to each other through a ...
Text Solution
|
- The tension in the string shown in figure m-2m to F is.
Text Solution
|