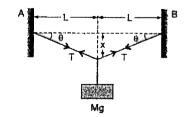
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A steel wire of diameter 0.8 mm and length 1 m is champed firmly at tw...
Text Solution
|
- Fig show two bodies A and B of masses 2.5 kg and 2.8 kg respectively f...
Text Solution
|
- A steel of area of cross-section A and length 2L is calmped family bet...
Text Solution
|
- A steel wire of negligible mass, length 2I , cross sectional area 'A' ...
Text Solution
|
- स्टील का यंग प्रत्यास्थता गुणांक, पीतल से दोगुना है | एक ही लम्बाई तथा...
Text Solution
|
- After suspendind a body of mass 1 kg from a wire of negligible mass, l...
Text Solution
|
- 2L लंबाई और A अनुप्रस्थ काट वाला एक तार दो बिंदुओं के बीच क्षैतिज ...
Text Solution
|
- If the diameter of A wire is twice the same length as that of another ...
Text Solution
|
- A steel wire of diameter 0.8 mm and length 1m is clamped firmly at two...
Text Solution
|