Text Solution
Verified by Experts
Recommended Questions
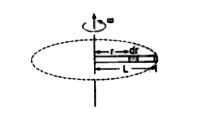
- A thin uniform metallic rod of length 0.5 m and radius. 0.1 m rotates ...
Text Solution
|
- A uniform rod of mass m and length l rotates in a horizontal plane wit...
Text Solution
|
- A thin uniform copper rod of length l and mass m rotates uniformly wit...
Text Solution
|
- A thin uniform metallic rod of length 0.5 m and radius 0.1 m rotates w...
Text Solution
|
- A rod of 1.5m length and uniform density 10^(4)kg//m^(3) is rotating a...
Text Solution
|
- A thin rod of length 3 m is being rotated with 10 rad/sec about its on...
Text Solution
|
- A uniform rod of mass m. length L, area of cross- secticn A is rotated...
Text Solution
|
- A thin uniform copper rod of length l and cross-section area A and mas...
Text Solution
|
- If the young's modulus of the material of the rod is 2 xx 10^(11) N//m...
Text Solution
|