A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
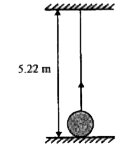
- A sphere of radius 0.1 m and mass 8pi kg is attached to the lower end...
Text Solution
|
- A sphere of radius 0.1m and mass 8 pi kg is attached to the lower end ...
Text Solution
|
- A sphere of radius 10 cm and mass 25 kg is attached to the lower en...
Text Solution
|
- A sphere of radius 0.1m and mass 8 pi kg is attached to the lower en...
Text Solution
|
- 0.1m ব্যাসার্ধবিশিষ্ট ও 8pi kg ভরবিশিষ্ট একটি গোলোককে ঘরের সিলিং থেকে ...
Text Solution
|
- A sphere with a diameter of 0.1m and a mass of 8pi kg is hung from the...
Text Solution
|
- A sphere of mass 2 kg and diameter 4.5 cm is attached to the lower and...
Text Solution
|
- A sphere of radius 0.1 m and mass 8 pi kg is attached to the lower end...
Text Solution
|
- A sphere of radius 0.1 m and mass 8 pi kg is attached to the lower end...
Text Solution
|