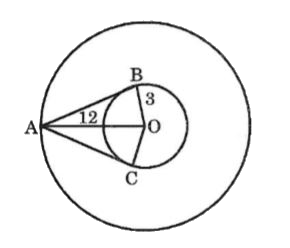
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- C(1) and C(2) are two concentric circles with centres at O. Their radi...
Text Solution
|
- Let C(1) and C(2) be externally tangent circles with radius 2 and 3 re...
Text Solution
|
- Transverse common tangents are drawn from O to the two circles C(1),C(...
Text Solution
|
- Let C(1) and C(2) be two circles with C(2) lying inside C(1) circle C ...
Text Solution
|
- C(1) तथा C(2) संकेन्द्रीय वृत्त हैं जिनका केन्द्र O हैं। जिनकी त्रिज्...
Text Solution
|
- Let C(1), C(2) be two circles touching each other externally at the p...
Text Solution
|
- C(1) and C(2) are two concentrate circles, the radius of C(2) being t...
Text Solution
|
- The centres of two circles C(1) and C(2) each of unit radius are at a...
Text Solution
|
- The circle C(1) : x^(2) + y^(2) = 3 , with centre at O , intersects...
Text Solution
|