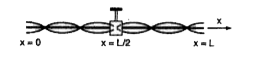In rods, like strings, clamped point is a node while the free ends are antinodes. So the situation, in accordance with given conditions is as shown in figure.
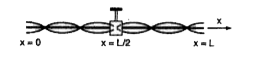
Now as distance between two consecutive nodes is `(lambda)/(2)` while between a node and an antinode is `(lambda)/(4)`.
`4xx[(lambda)/(2)] +2[(lambda)/(4)]=L, "i.e., "lambda=(2xx1)/(5)=0.4m .........(i)`
Also as `Y=2xx10^(11)N//m^(2) and rho=8xx10^(3)kg//m^(3)`
`v= sqrt((Y)/(rho))= sqrt((2xx10^(11))/(8xx10^(3)))=5000 m//s`
So, from `v=f lambda, f=((v)/(lambda))= ((5000)/(0.4))=12500Hz .............(ii)`
Now if incident and reflected waves along the rod are `y_(1)=A sin (omegat-kx) and y_(2)=A sin (omega t +kx +phi)`, resultant wave will be:
`y=y_(1)+y_(2)=A[sin (omegat-kx)+sin(omega t+kx +phi)]`
But as `sinC+sinD=2"sin"((C+D))/(2)"cos"((C-D))/(2)`
`y=2A cos[kx+(phi)/(2)]sin[omega t+(phi)/(2)]`
Now as free end of the rod is an antinode, i.e., amplitude is max at x=0, so that
`cos[k xx 0+(phi)/(2)]= "max"=1, "i.e.," phi=0`
and `A_("max")=2A = 2xx10^(-6)m` (given)
So, `y=2xx10^(-6)coskx sin omega t`
or `y=2xx10^(-6) cos [(2pi)/(lambda)x] sin 2pi f t" "["as k"=(2pi)/(lambda) and omega =2pi f]`
Above equation in the light of Eqns. (i) and (ii) reduces to
`y=2xx10^(-6) cos 5pi x sin25000pi t ..........(iii)`
Now as for a point 2 cm from the mid-point `x =(0.50 pm0.02)`.
`y=2xx10^(-6)cos5pi (0.50pm 0.02 ) sin 25000pi t`
This is the required result.
Now as `2cos A sinB = sin (A+B) - sin(A-B)`
the resultant wave `y= 2xx10^(-6) cos (5pi x) sin (25000pi t)` can be written as
`y=10^(-6) [sin (5pi x +25000pi t)-sin(5pi x-25000pi t)]`
i.e., `y=10^(-6)sin[2500pi t+5pi x] + 10^(-6) sin[25000pi t+5pi x] [ " as "sin(-theta)= -sin theta]`
or `y=y_(1)+y_(2)" with "y_(1)=10^(-6) sin[25000pi t+5pi x]`
and `y_(2)=10^(-6) sin[25000pi t-5pi x]` representing the required constituent waves.