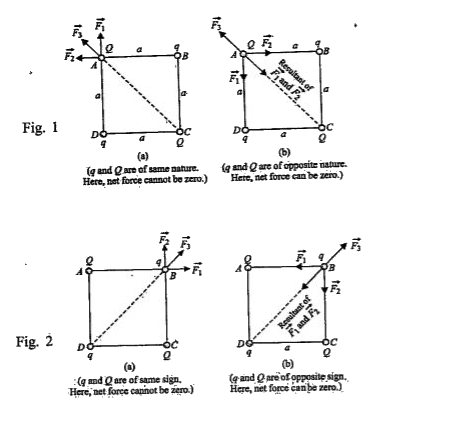
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Point charges are placed at the vertices of a square of side 'a' as sh...
Text Solution
|
- Three charges Q, +q and +q are placed at the vertices of a right-angle...
Text Solution
|
- Point charge are placed at the verticas of a squre of side a as shown ...
Text Solution
|
- Three charges Q, (+q) and (+q) are placed at the vertices of an equila...
Text Solution
|
- Three charges Q, +q and +q are placed at the vertices of a right angle...
Text Solution
|
- Assertion : Five charges +q each are placed at five vertices of a regu...
Text Solution
|
- Three charges Q, +q and +q are placed at the vertices of a right-angle...
Text Solution
|
- Consider the charge q, q and -q placed at the vertices of an equilater...
Text Solution
|
- The charges Q, +q and + q are placed at the vertices of an equilateral...
Text Solution
|