A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
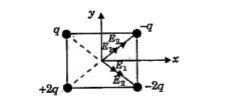
- Four charges +q,-q,-2q and +2q are kept in the corners of a square of ...
Text Solution
|
- The corners A, B, C, and D of a square are occupied by charges q,-q,2Q...
Text Solution
|
- Four point charges -Q, -q, 2q and 2Q are placed, one at each corner of...
Text Solution
|
- Four charges +q,+2q,+3q and +4q are placed at the four corners ABCD of...
Text Solution
|
- किसी वर्ग के चारों कोनों पर बिंदु आवेश -Q, -q, 2q तथा 2Q रखे गए हैं। Q...
Text Solution
|
- Four charge +2q, - 2q,-3q and +3q are kept in the comers of a squa...
Text Solution
|
- Find the electric field and potential at the centre of a square of sid...
Text Solution
|
- q,2q, 3q and 4q charges are placed at the four corners A,B,C and D of ...
Text Solution
|
- Four point charges -Q, -q, 2q and 2Q are placed, one at each corner of...
Text Solution
|