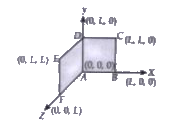A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A loop, made of straight edges has six corners at A(0,0,0), B(L,0,0) ,...
Text Solution
|
- A loop made of straight edegs has six corners at A(0,0,0), B(L, O,0) C...
Text Solution
|
- मूल्यांकन कीजिए - |(a,l,m,n),(0,b,p,q),(0,0,c,r),(0,0,0,d)|
Text Solution
|
- A loop, made of straight edges has six corners at A(0,0,0), B(L,0,0), ...
Text Solution
|
- If A=[((k)/(2),0,0),(0,(l)/(2),0),(0,0,(m)/(4))] and A^(-1)= [((1)/(2)...
Text Solution
|
- A loop ABCA of straight edges has three corner points A (8, 0, 0), B (...
Text Solution
|
- सीधी कोरों से बने एक लूप में A(0, 0, 0), B(L, 0, 0), C(L, L, 0), D(0, ...
Text Solution
|
- एक लूप सीधी भुजाओं से बना है, जिसमें छः कोने A(0,0,0), B(L,0,0),C(L, L...
Text Solution
|
- A loop, made of straight edges has six corners at A(0,0,0), B(L,0,0) ,...
Text Solution
|