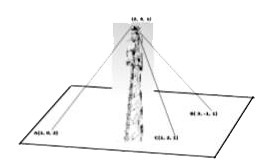
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A mobile tower stands at the top of a hill. Consider the surface on w...
Text Solution
|
- A tower stands at the centre of a circular park. A and B are two point...
Text Solution
|
- A tower of height 50 metres stands on a level ground.A flag-staff stan...
Text Solution
|
- A tower stands at the top of a hill whose height is three times the he...
Text Solution
|
- A tower stands vertically on the ground. From a point on the ground...
Text Solution
|
- From the top of a tower the angle of depression of a point on ...
Text Solution
|
- A tower stands vertically on the ground. From a point on the ground wh...
Text Solution
|
- A tower stands vertically on the ground. From a point on the ground, ...
Text Solution
|
- A tower stands vertically on the ground. From a point on the ground...
Text Solution
|