Home
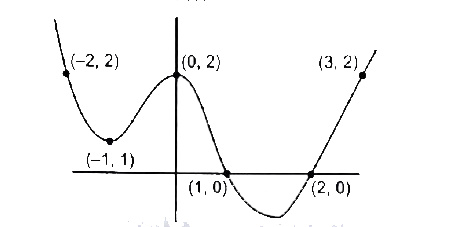
Class 10
MATHS
In the given figure graph of : y =p (x...

In the given figure graph of :
`y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ ….. + a _(n)` is given.

The product of all imaginary roots of `p(x) =0` is:

A

1

B

2

C

3

D

4

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • SAMPLE PAPER 02

    EDUCART PUBLICATION|Exercise SECTION - A|11 Videos

  • SAMPLE PAPER 02

    EDUCART PUBLICATION|Exercise SECTION - A Fill in the blanks|6 Videos

  • SAMPLE PAPER 02

    EDUCART PUBLICATION|Exercise SECTION-B|20 Videos

  • SAMPLE PAPER 01

    EDUCART PUBLICATION|Exercise PART-B (SECTION-V)|4 Videos

  • SAMPLE PAPER 03

    EDUCART PUBLICATION|Exercise Section - C|10 Videos

Similar Questions

Explore conceptually related problems

In the given figure graph of : y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n) is given. The minimum number of real roots of equation (p' (x))^(2) +p(x)p''(x) =0 are:

In the given figure graph of : y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n) is given. If p (x) + k=0 has 4 distinct real roots alpha, beta, gamma,delta then [alpha]+[beta]+[gamma]+[delta], (where [.] denotes greatest integer function) is equal to:

Differentiate |x|+a_(0)x^(n)+a_(1)x^(n-1)+a_(2)x^(n-1)+...+a_(n-1)x+a_(n)

Differentiate the following with respect of x:a_(0)x^(n)+a_(1)x^(n-1)+a_(2)x^(n-2)++a_(n-1)x+a_(n)

(1+x)^(n)=a_(0)+a_(1)x+a_(2)*x^(2)+......+a_(n)x^(n) then prove that

Let f(x)=a_(0)x^(n)+a_(1)x^(n-1)+a_(2)x^(n-2)+......+a_(n),(a_(0)!=0) if a_(0)+a_(1)+a+_(2)+......+a_(n)=0 then the root of f(x) is

If (1 + x + x^(2) + x^(3))^(n) = a_(0) + a_(1)x + a_(2)x^(2)+"……….."a_(3n)x^(3n) then which of following are correct

a_(0)f^(n)(x)+a_(1)f^(n-1)(x)*g(x)+a_(2)f^(n-2)g^(2)(x)+......+a_(n)g^(n)(x)>=0

Let f(x) = a_(0)x^(n) + a_(1)x^(n-1) + a_(2) x^(n-2) + …. + a_(n-1)x + a_(n) , where a_(0), a_(1), a_(2),...., a_(n) are real numbers. If f(x) is divided by (ax - b), then the remainder is

Let (1 + x^(2))^(2) (1 + x)^(n) = a_(0) + a_(1) x + a_(2) x^(2) + … if a_(1),a_(2) " and " a_(3) are in A.P , the value of n is