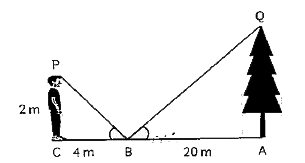
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SAMPLE PAPER 5
EDUCART PUBLICATION|Exercise PART - A (SECTION - I) |21 VideosSAMPLE PAPER 5
EDUCART PUBLICATION|Exercise PART - A (SECTION - II) |20 VideosSAMPLE PAPER 5
EDUCART PUBLICATION|Exercise SECTION - B|20 VideosSAMPLE PAPER 4
EDUCART PUBLICATION|Exercise PART-B(SECTION-V)|5 VideosSAMPLE PAPER 6
EDUCART PUBLICATION|Exercise SECTION- C |10 Videos
Similar Questions
Explore conceptually related problems
EDUCART PUBLICATION-SAMPLE PAPER 5-SECTION - C
- Magnification of figures is a process of enlarging the apparent size, ...
Text Solution
|
- Magnification of figures is a process of enlarging the apparent size, ...
Text Solution
|
- Magnification of figures is a process of enlarging the apparent size, ...
Text Solution
|
- Magnification of figures is a process of enlarging the apparent size, ...
Text Solution
|
- Magnification of figures is a process of enlarging the apparent size, ...
Text Solution
|
- When we pass from crossing on a road we all see traffic lights blinkin...
Text Solution
|
- When we pass from crossing on a road we all see traffic lights blinkin...
Text Solution
|
- Factor tree of a number helps in calculating
Text Solution
|
- When we pass from crossing on a road we all see traffic lights blinkin...
Text Solution
|
- Two numbers which do not have any factor common other than 1 are calle...
Text Solution
|