Home
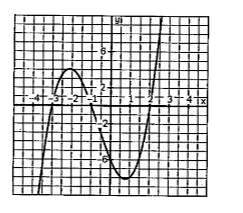
Class 10
MATHS
Find the zeroes of the curve....


Find the zeroes of the curve.

A

`-3, -6, -1`

B

`2, -6, -1`

C

`-3, -1, 2`

D

`3, 1, -2`

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • SAMPLE PAPER 1

    EDUCART PUBLICATION|Exercise Section -A|20 Videos

  • SAMPLE PAPER 1

    EDUCART PUBLICATION|Exercise Section -B|20 Videos

  • SAMPLE PAPER 1

    EDUCART PUBLICATION|Exercise SECTION B|20 Videos

  • SAMPLE PAPER 07

    EDUCART PUBLICATION|Exercise SECTION -C|10 Videos

  • SAMPLE PAPER 10

    EDUCART PUBLICATION|Exercise SECTION-C|10 Videos

Similar Questions

Explore conceptually related problems

_______ helps in finding the areas of the curves.

A curve is such that the length of the polar radius of any point on the curve is equal to the length of the tangent drawn at this point.Form the differential equation and solve it to find the equation of the curve.

The slope of the tangent at a point P(x, y) on a curve is (- (y+3)/(x+2)) . If the curve passes through the origin, find the equation of the curve.

The slope of tangent at a point P(x, y) on a curve is - x/y . If the curve passes through the point (3, -4) , find the equation of the curve.

Find the area under the curve

Find the quadratic polynomial, the sum of whose zeros is (5/2) and their product is 1 . Hence, find the zeros of the polynomial.

Find the quadratic polynomial, the sum of whose zeros is sqrt2 and their product is -12 . Hence, find the zeros of the polynomial.

A curve passes through the point (3,-4) and the slope of.the is the tangent to the curve at any point (x,y) is (-(x)/(y)) .find the equation of the curve.

The normal at the point (2,(1)/(2)) on the curve xy=1, meets the curve again at Q. If m is the slope of the curve at Q. then find |m|

Find the quadratic polynomial, the sum of whose zeros is 0 and their product is -1. Hence, find the zeros of the polynomial.