Home
Class 10
MATHS
In figure , is shown a sector OAP of a c...

In figure , is shown a sector OAP of a circle with centre O , containing `angletheta` . AB is perpendicular to the radius OA and meets OP produced at B . Prove that the perimeter of shaded region is `r [ tan theta + sec theta - 1- (pi theta)/(180)]`

Promotional Banner

Topper's Solved these Questions

  • DIKSHA QUESTIONS

    OSWAL PUBLICATION|Exercise UNIT -VI: Area Related to Circle (Surface Areas and volumes) (MULTIPLE CHOICE QUESTIONS)|3 Videos

  • DIKSHA QUESTIONS

    OSWAL PUBLICATION|Exercise UNIT -VI: Area Related to Circle (Surface Areas and volumes) (VERY SHORT ANSWER TYPE QUESTIONS)|4 Videos

  • DIKSHA QUESTIONS

    OSWAL PUBLICATION|Exercise UNIT -VI: Area Related to Circle (Areas Related to Circles ) ( SHORT ANSWER TYPE QUESTIONS )|17 Videos

  • COORDINATE GEOMETRY

    OSWAL PUBLICATION|Exercise SELF ASSESSMENT |20 Videos

  • INTRODUCTION TO TRIGONOMETRY

    OSWAL PUBLICATION|Exercise Self - Assessment |15 Videos

Similar Questions

Explore conceptually related problems

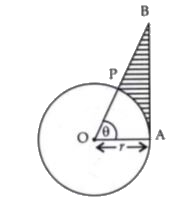
In the given figure,is shown a sector OAP of a circle with centre 0, containing /_ theta. AB is perpendicular to the radius OA and meets OP produced at B.Prove that the perimeter of shaded region is r[tan theta+sec theta+pi(theta)/(180)-1]

Figure shows a sector of a circle,centre O, containing an angle theta. Prove that ( i) Perimeter of the shaded region is r(tan theta+sec theta+(pi theta)/(180)-1)( ii) Area of shaded region is (r^(2))/(2)(tan theta-pi(theta)/(180))

Fig. 15.17, shows a sector of a circle, centre O , containing an angle thetao , prove that: (FIGURE) (i) Perimeter of the shaded region is r\ (tantheta+sectheta+(pitheta)/(180)-1) (ii) Area of the shaded region is (r^2)/2\ (tantheta-(pitheta)/(180))

Figure shows a sector of a circle of radius r containing an angle theta^(@) The area of the sector is Acm^(2) and the perimeter is 50cm. Prove that theta=(360)/(pi)((25)/(r)-1) and A=25r-r^(2)

In figure , AB and CD are two diameters of a circle ( with centre O) perpendicular to each other and OD is the diameter of the smaller circle . If OA = 7 cm , find the area of the shaded region.

If Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.

In the given figure,AB and CD are two diameters of circles (with centre O) Perpendicular to each other and OD is the diameter of the smallest circle.If OA = 7cm, Find the area of the shaded region.

In the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

In the adjoining figure O is the centre of the circle with radius 'r' AB, CD and EF are the diameters of the circle. angleOAF = angleOCB = 60^(@) . What is the area of the shaded region?