Home
Class 10
MATHS
A stop sign is an example of a Polygon. ...

A stop sign is an example of a Polygon. In the image , you can see examples of diagonals in geometry n the stop sign, there a various number of diagonals possible in a Polygon.

the number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated.


By considering the pattern, the value of 'p' is

A

11

B

13

C

14

D

15

Text Solution

Verified by Experts

Promotional Banner

Topper's Solved these Questions

  • SAMPLE PAPER 13

    EDUCART PUBLICATION|Exercise PART B (SECTION-III)|8 Videos

  • SAMPLE PAPER 13

    EDUCART PUBLICATION|Exercise PART B (SECTION-IV)|6 Videos

  • SAMPLE PAPER 13

    EDUCART PUBLICATION|Exercise PART - B (SECTION - V)|4 Videos

  • SAMPLE PAPER 11 (SELF - ASSESSMENT)

    EDUCART PUBLICATION|Exercise SECTION -C|10 Videos

  • SAMPLE PAPER 2

    EDUCART PUBLICATION|Exercise SECTION - D |9 Videos

Similar Questions

Explore conceptually related problems

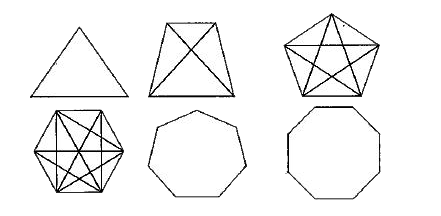
A stop sign is an example of a Polygon, in the image, you can see examples of diagonals in geometry in the stop sign. Hence, there a various number of diagonals possible in a Polygon. The number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated. On the basis of the above information, answer any four of the following questions: For a polygon, d and n are related as d = An^(2) + Bn . The relations for a triangle and a quadrilateral are

A stop sign is an example of a Polygon, in the image, you can see examples of diagonals in geometry in the stop sign. Hence, there a various number of diagonals possible in a Polygon. The number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated. On the basis of the above information, answer any four of the following questions: By considering the pattern, the value of q' is

The number of diagonals in a polygon is 20. The number of sides of the polygon is

In a polygon the number of diagonals is 54. the number of sides of the polygon, is

Write the number of diagonals of an n-sided polygon.