Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-LINEAR PROGRAMMING-EXERCISE
- A soft drinks firm has two bottling plants, one located at P and the l...
Text Solution
|
- A toy company manufactures two types of dolls, A and B. Market tests a...
Text Solution
|
- A dietician wishes to mix together two kinds of food X and Y in such a...
Text Solution
|
- (Diet problem)A dietician has to develop a special diet using two food...
Text Solution
|
- (Diet problem)A dietician has to develop a special diet using two food...
Text Solution
|
- A fruit grower can use two types of fertilizer in his garden, brand P ...
Text Solution
|
- A fruit grower can use two types of fertilizer in his garden, brand P ...
Text Solution
|
- A factory owner purchases two types of machines A and B for his factor...
Text Solution
|
- A manufacturer has three machines I, II and III installed in his facto...
Text Solution
|
- A manufaturer makes two types of toys, A and B cups. Three machines ar...
Text Solution
|
- A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs ...
Text Solution
|
- A packet of plain biscuits costs Rs 6 and that of chocolate bisuits co...
Text Solution
|
- The graph of the inequation 2x+3yge6 does not lie in the first quadran...
Text Solution
|
- The graph of the inequation 3x+2y>6 does not lie in the fourth quadran...
Text Solution
|
- The objective function is maximum or minimum at a point, which lies on...
Text Solution
|
- Maximize Z=x+2y subject to : x+yge5, xge0,yge0
Text Solution
|
- Maximize Z=4x+y subject to : x+yle50, x,yge0
Text Solution
|
- What is optimum solution?
Text Solution
|
- What is objective function?
Text Solution
|
- What is feasible region?
Text Solution
|
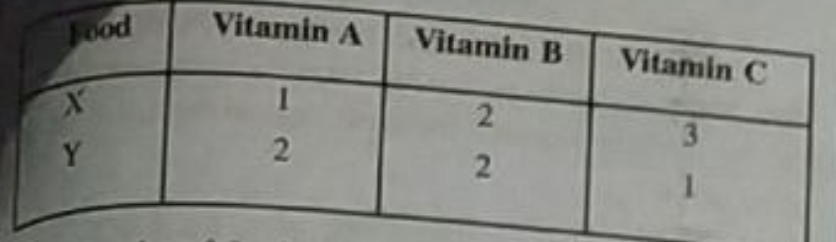 One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?
One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?