Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT TELUGU-CIRCLES-Examples
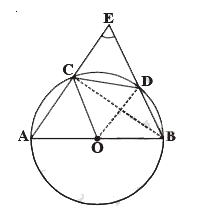
- In figure, bar(AB) is a diameter of the circle, bar(CD) is a chord equ...
Text Solution
|
- Construct a circumcircle of the triangle ABC where AB = 5cm, angleB = ...
Text Solution
|
- In the figure, O is the centre of the circle. Find the length of CD, i...
Text Solution
|
- In the adjacent figure, there are two concentric circles with centre ‘...
Text Solution
|
- Let ‘O’ be the centre of a circle, PQ is a diameter, then prove that a...
Text Solution
|
- Find the value of x^(@) in the adjacent figure.
Text Solution
|
- In the figure, angleA=120^(@) then find angleC ?
Text Solution
|
- In figure, bar(AB) is a diameter of the circle, bar(CD) is a chord equ...
Text Solution
|