Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TRIANGLES
EDUCART PUBLICATION|Exercise VERY SHORT QUESTIONS|10 VideosTRIANGLES
EDUCART PUBLICATION|Exercise SHORT ANSWER (SA-I) TYPE QUESTIONS|30 VideosTRIANGLES
EDUCART PUBLICATION|Exercise LONG ANSWER TYPE QUESTIONS|10 VideosSURFACE AREAS AND VOLUMES
EDUCART PUBLICATION|Exercise LONG ANSWER TYPE QUESTIONS|30 Videos
Similar Questions
Explore conceptually related problems
EDUCART PUBLICATION-TRIANGLES-OBJECTIVE TYPE QUSTIONS (FILL IN THE BLANKS)
- Let ABC ~ triangle DEF and their areas be 81 cm^(2) and 144 cm^(2). If...
Text Solution
|
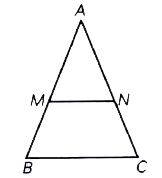
- In the figure, MN |\| BC " and " AM : MB = 1 : 3, " then " (ar(triang...
Text Solution
|
- In Delta ABC, AB=6 sqrt(3) cm, AC=12 cm and BC=6 cm. Then angle B is
Text Solution
|
- Two triangles are similar if their corresponding sides are ………….
Text Solution
|
- A ladder 10m long reaches a window 8 m above the ground. Find the d...
Text Solution
|
- In an equilateral triangle of side 2a, calculate the length of its alt...
Text Solution
|
- The perimeters of tow similar triangles DeltaABC and DeltaPQR are...
Text Solution
|
- The length of an altitude in an equilateral triangle of side 'o' cm is...
Text Solution
|
- If areas of two similar triangles are equal, then these triangles are…...
Text Solution
|
- A diagonal of a parallelogram divides it into two triangles of equal a...
Text Solution
|
- If S is a point on side PQ of a triangle PQR such that PS = QS = RS, ...
Text Solution
|