A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
EDUCART PUBLICATION-SAMPLE PAPER 7-SECTION -C
- Which of the following is correct regarding f(x) = x^(3) ?
Text Solution
|
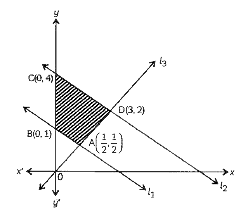
- The feasible region of a system of linear inequalities is shown shaded...
Text Solution
|
- If A = [ (1,2,-3),(2,3,2),(3,-3,-4)] then A^(-1) if it exists is :
Text Solution
|
- If the curves ay +x^(2) =7 and x^(3) =y cut orthogonally at (1,1) then...
Text Solution
|
- If A is a invertible matrix of order 4 then |A^(-1)|=
Text Solution
|
- A man has Rs 35000 which the want to invest in two different types of ...
Text Solution
|
- A man has Rs 35000 which the want to invest in two different types of ...
Text Solution
|
- A man has Rs 35000 which the want to invest in two different types of ...
Text Solution
|
- A man has Rs 35000 which the want to invest in two different types of ...
Text Solution
|
- A man has Rs 35000 which the want to invest in two different types of ...
Text Solution
|