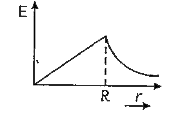
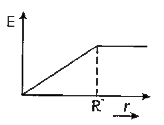
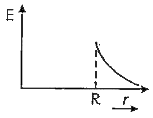
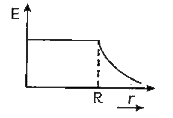
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
EDUCART PUBLICATION-SAMPLE PAPER 6-Section-C
- vec(E ) due to uniformly charged sphere of radius R as a function of d...
Text Solution
|
- If two conductors carry current in opposite direction, then:
Text Solution
|
- Emf induced in the left arm of the loop, if it is moved out of the mag...
Text Solution
|
- Case Study: Read the following paragraph and answer the questions. S...
Text Solution
|
- Case Study: Read the following paragraph and answer the questions. S...
Text Solution
|
- Case Study: Read the following paragraph and answer the questions. S...
Text Solution
|
- Case Study: Read the following paragraph and answer the questions. S...
Text Solution
|