Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
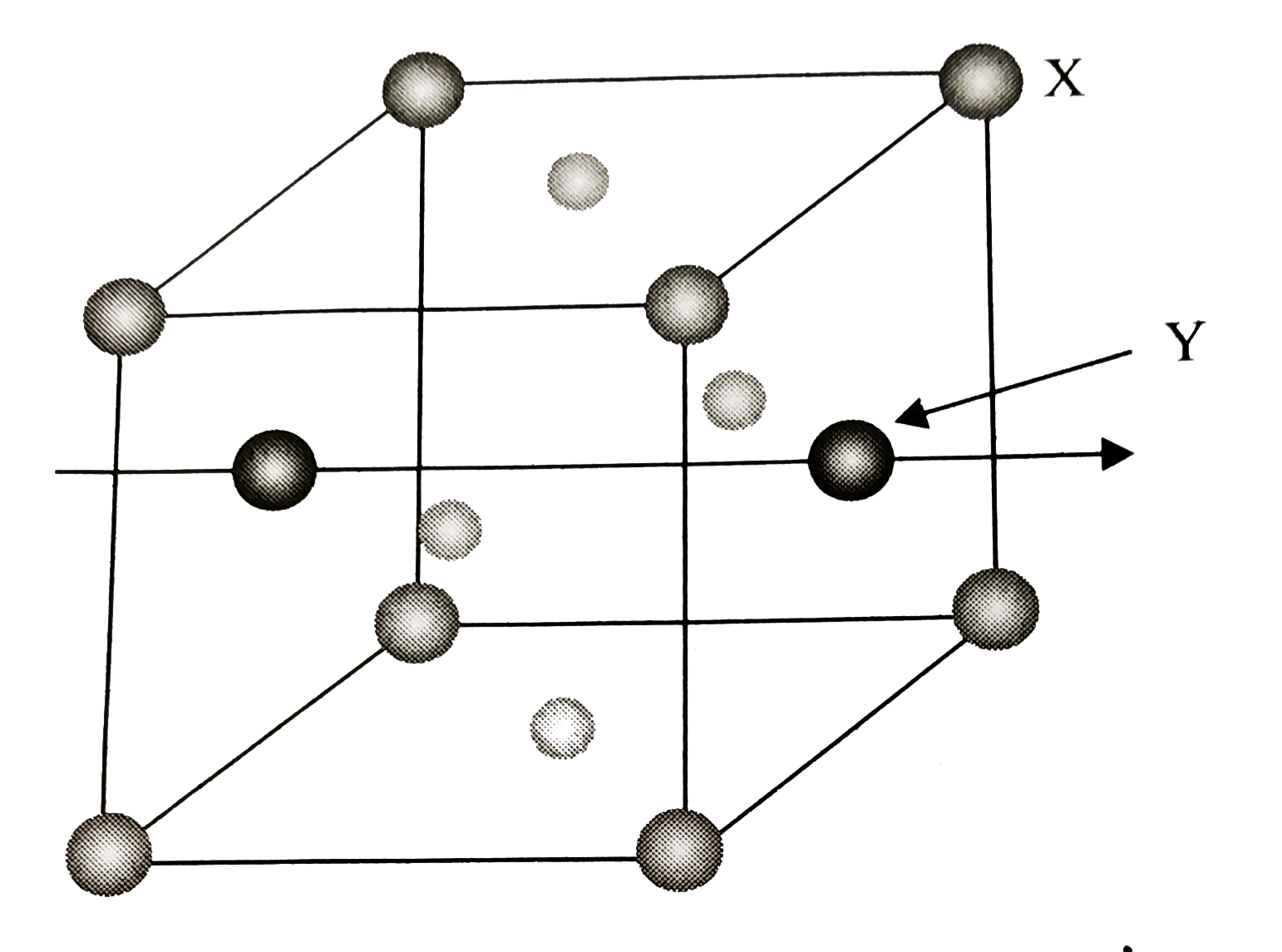
- A compound formed by elements X and Y has a cubic structure in which ...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which ...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|