a. `Z_(eff(X)) = (n_(c))/(8) + (n_(f))/(2) = (8)/(8) + (6)/(2) = 1 + 3 = 4`
`Z_(eff(Y)) = (n_(b))/(8) + (n_(e))/(4) = (1)/(1) + (12)/(4) = 1 + 3 = 4`.
`Z_(eff(X + Y)) = 4 + 4 = 8`
ii. Total number of atoms in the cube
ii. `= 8` (corners) `+ 6 ("face centre") + 1` (body centre)
`+ 12` (edge centre)
`= 27` atoms/units cube
(iii). Formula: `Z_(eff(X)) = 4, Z_(eff(Y)) = 4`
implies `X_(4) Y_(4) = 4XY`
b. i.
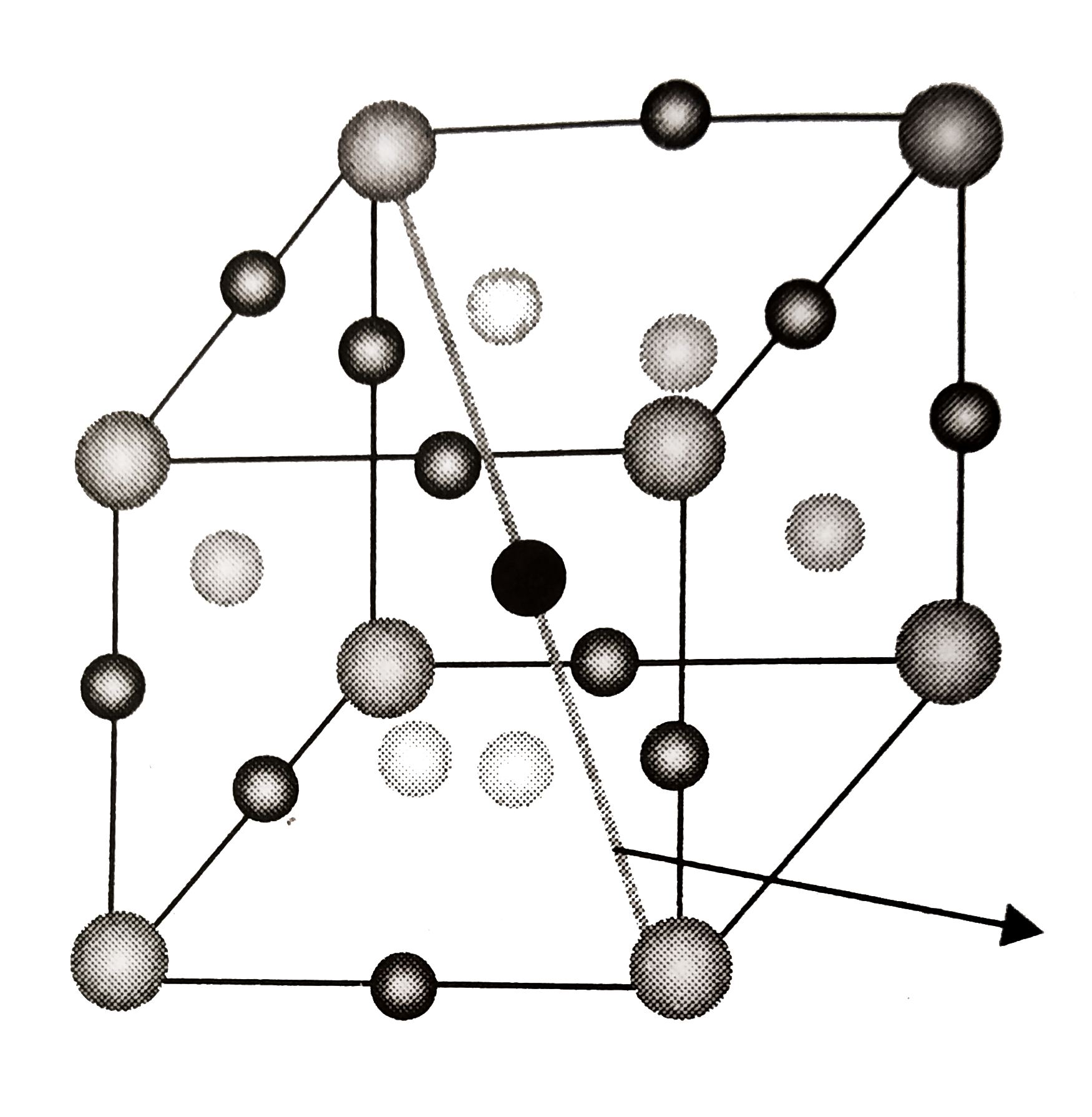
Atoms removed from one body diagonal
`= 2` atom form corner `+ 1` atom form body centre
`= 3` atoms. `Z_(eff(X)) = (n_(c))/(8) + (n_(f))/(2) = (8 - 2)/(8) + (6)/(2) = (15)/(4)`
`Z_(eff(Y)) = (n_(b))/(8) +(n_(c))/(4) = (1 - 1)/(1) + (12)/(4) = 0 + 3 = 3`
`Z_(eff(X + Y)) = (15)/(4) + 3 = (27)/(4)`
ii. Total number of atoms in the cube
`= 6 ("corner") + 6 ("face centre") +` Zero (body centre) `+ 12` (edge centres)
`= 24` atoms/unit cube
iii. `Z_(eff(X)) = (15)/(4), Z_(eff(Y)) = 3`
`implies X_((15/(4)) Y_(3)`.
Simplifying `X_(15) Y_(12)`
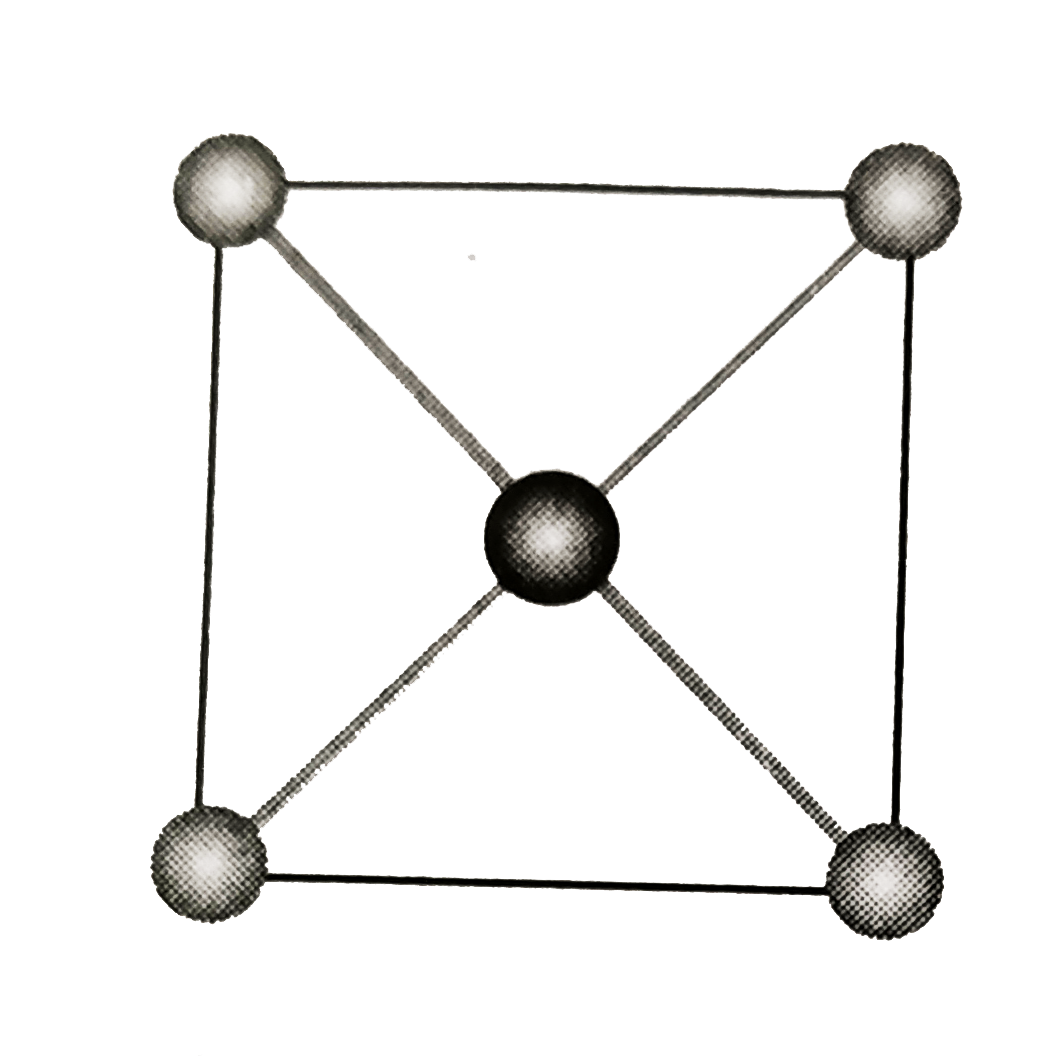
`Z_(eff(X)) = (n_(c)) /(8) + (n_(f))/(2) = (8 - 4)/(8) + (6 - 1)/(2) = 1 + 2 = 3`.
`Z_(eff(Y)) = (n_(b))/(8) +(n_(c))/(4) = (1 - 1)/(1) + (12)/(4) = 1 + 3 = 4`
`Z_(eff(X)) = 3 + 4 = 7`
ii. Total number of atoms in a cube
`= 4 ("corner") + 5 ("face centre") + 1` (body centre)
`+ 12` (edge centre)
`= 22` atoms/unit cube
iii. Formula: `Z_(eff(X)) = 3, Z_(eff(Y)) = 4`
`implies X_(3) Y_(4)`.
d. Plane passing through the middle of cube (other atoms are not shown)
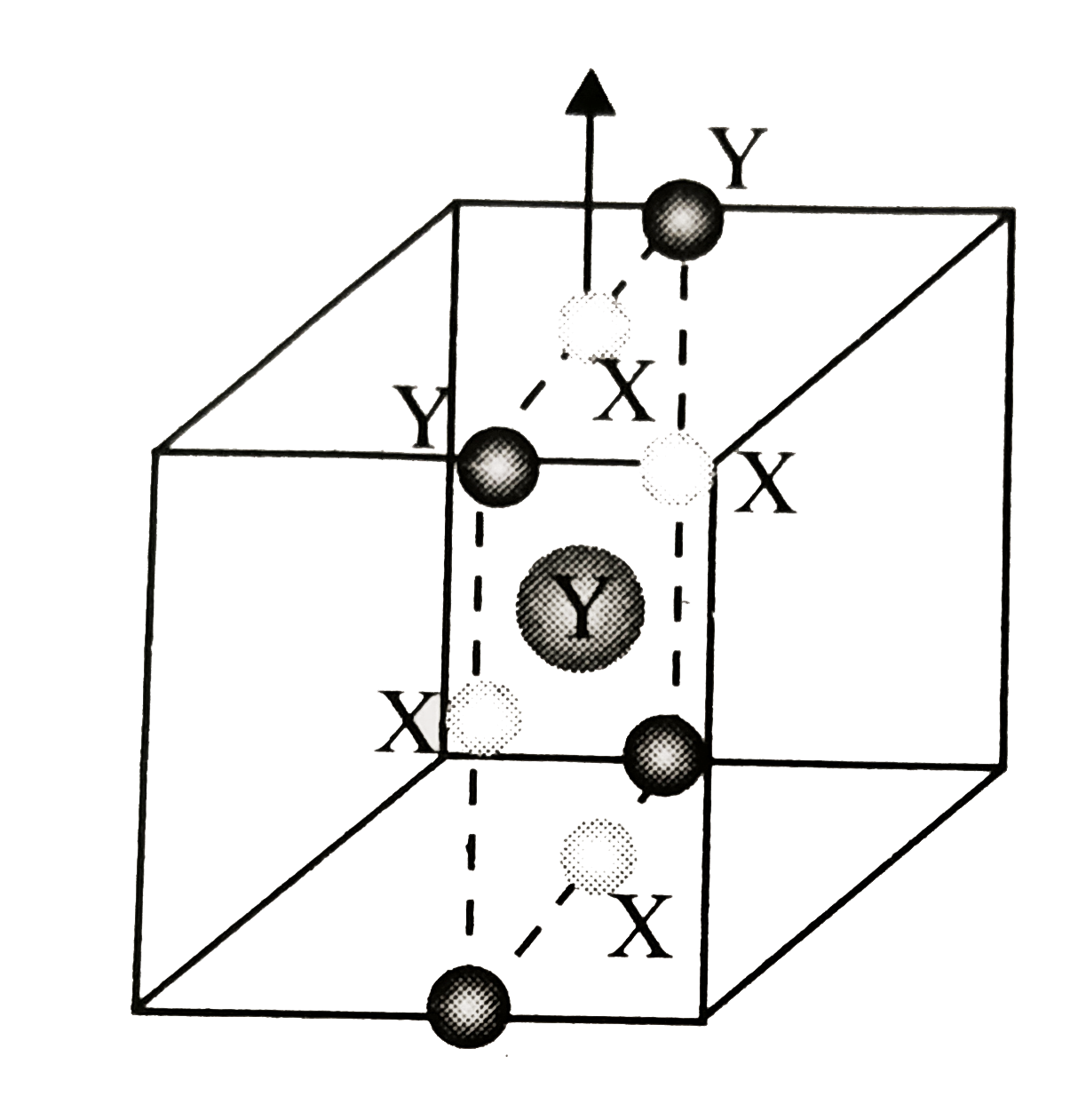
i. `Z_(eff(X)) = (n_(c)) /(8) + (n_(f))/(2) = (8)/(8) + (6 - 4)/(2) = 1 + 1 = 2`
`Z_(eff(Y)) = (n_(b))/(8) +(n_(c))/(4) = ((1 - 1))/(1) + ((12 - 4))/(4) = 2`.
`Z_(eff(X + Y)) = 2 + 2 = 4`
ii. Total number of the atoms in the cube
`= 8 ("corner") + 2 ("face centres") +` zero (body centre) `+ 8` (edge centres)
`= 18` atoms/unit cube
iii. Formula: `Z_(eff(X)) = 2, Z_(eff(Y)) = 2`
e.
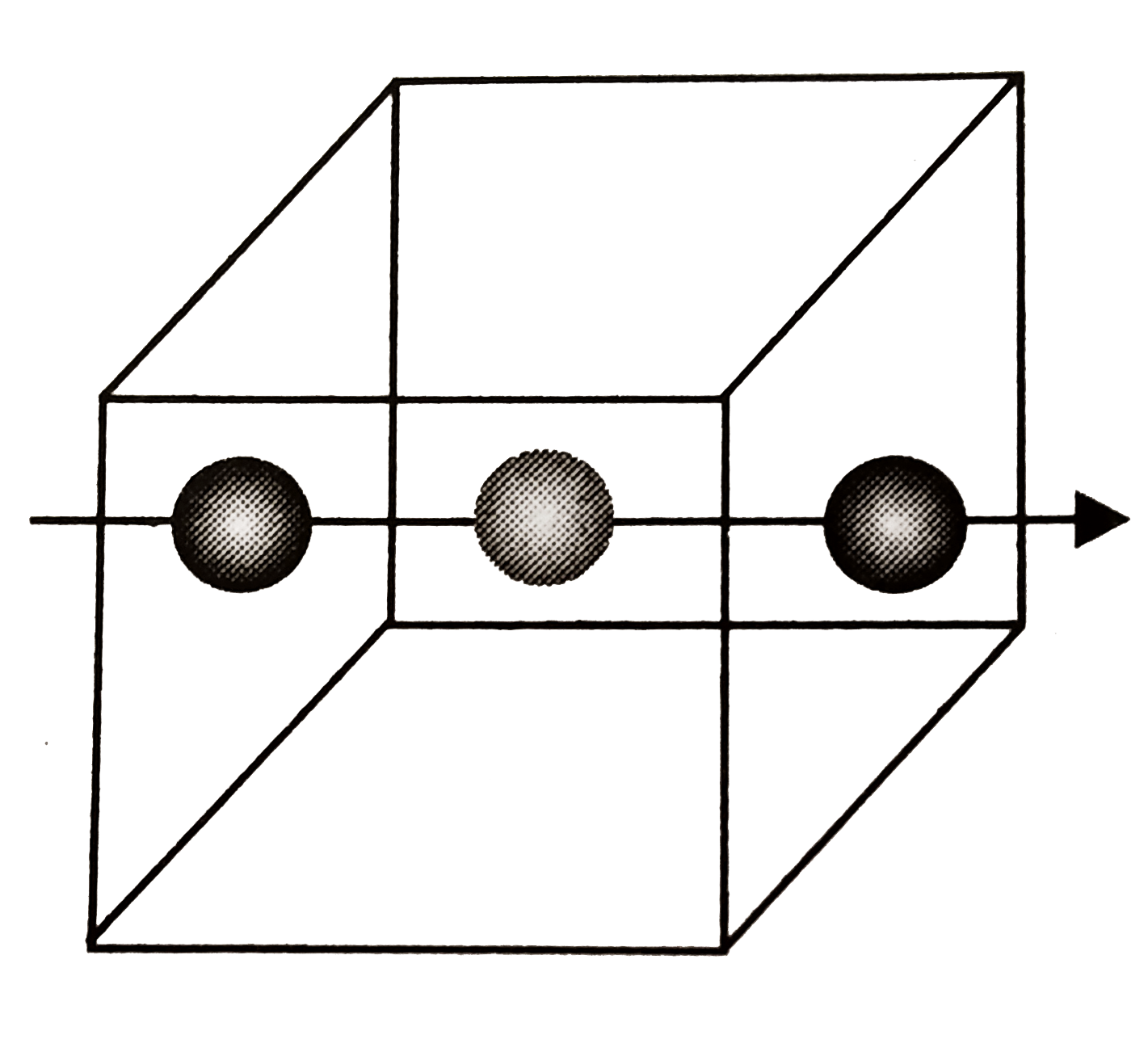
`Z_(eff(X)) = (n_(c)) /(8) + (n_(f))/(2) = (8)/(8) + ((6 - 2))/(2) = 1 + 2 = 3`
`Z_(eff(Y)) = (n_(b))/(8) +(n_(c))/(4) = ((1 - 1))/(1) + (12)/(4) = 0 + 3 = 3`.
`Z_(eff(X + Y)) = 3 + 3 = 6`.
ii. Total number atom in a cube `= 8` (corner) `+ 6` (face centre)
zero (body centre) `+ 12` (edge centre)
`= 24` atoms/unit cube
iii. Formula: `Z_(eff(X)) = 3, Z_(eff(Y)) = 3`
Formula is `X_(3) Y_(3)` or `3XY`.



