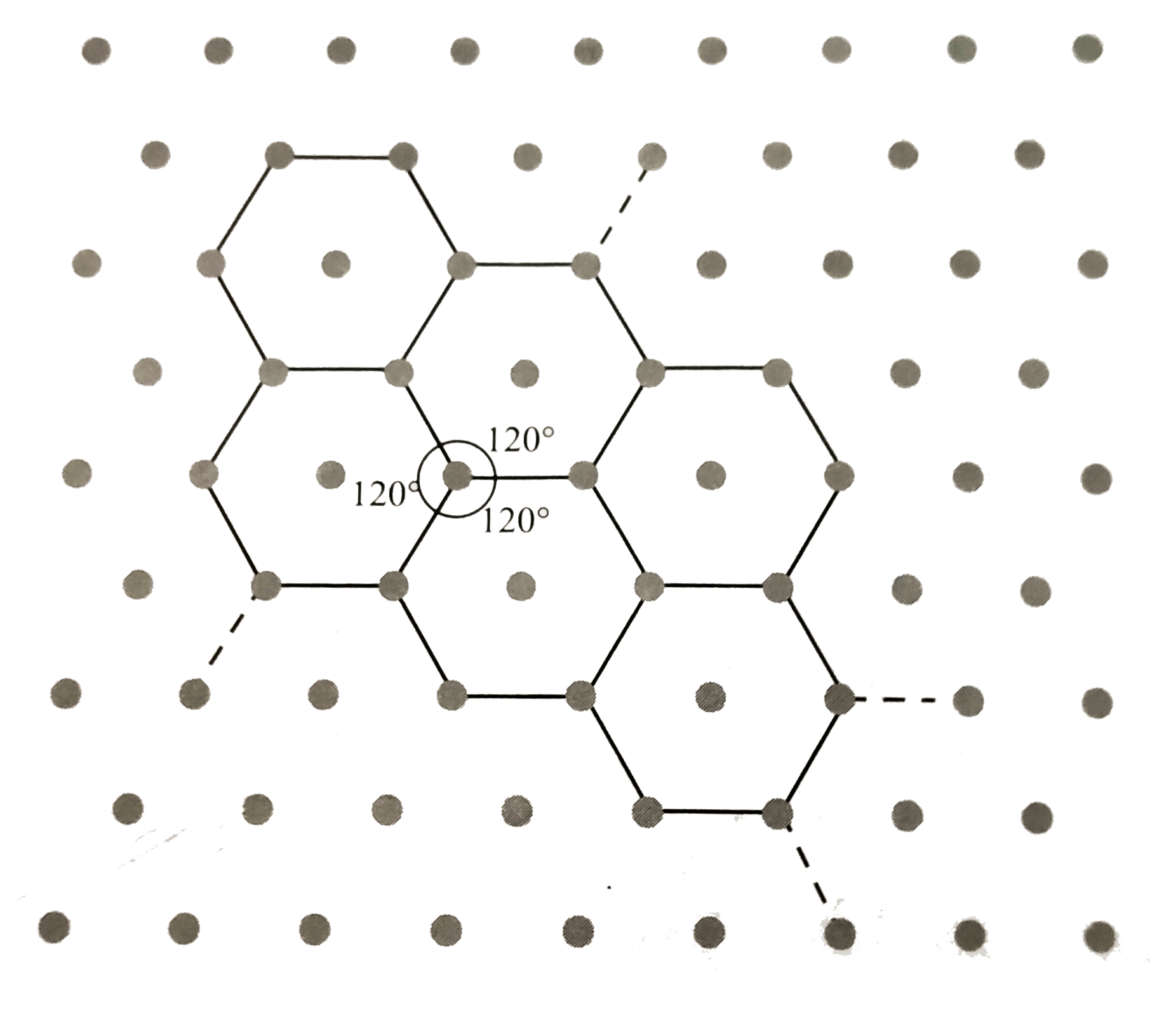
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Draw a two-dimesnsional haxagonal lattice. Try to visualize the possib...
Text Solution
|
- Which of the following statements is correct for a two-dimensional ha...
Text Solution
|
- How many types of two-dimensional lattice exist? Why pentagonal lattic...
Text Solution
|
- For two- dimensional hexagonal lattice, the unit cell is
Text Solution
|
- For two-dimensional hexagonal lattice, thee unit cell is
Text Solution
|
- How many three dimensional lattices are possible ?
Text Solution
|
- How many types of two-dimensional lattices are possible?
Text Solution
|
- How one and two-dimensional lattices are formed?
Text Solution
|
- The number of two dimensional lattice is-
Text Solution
|