Home
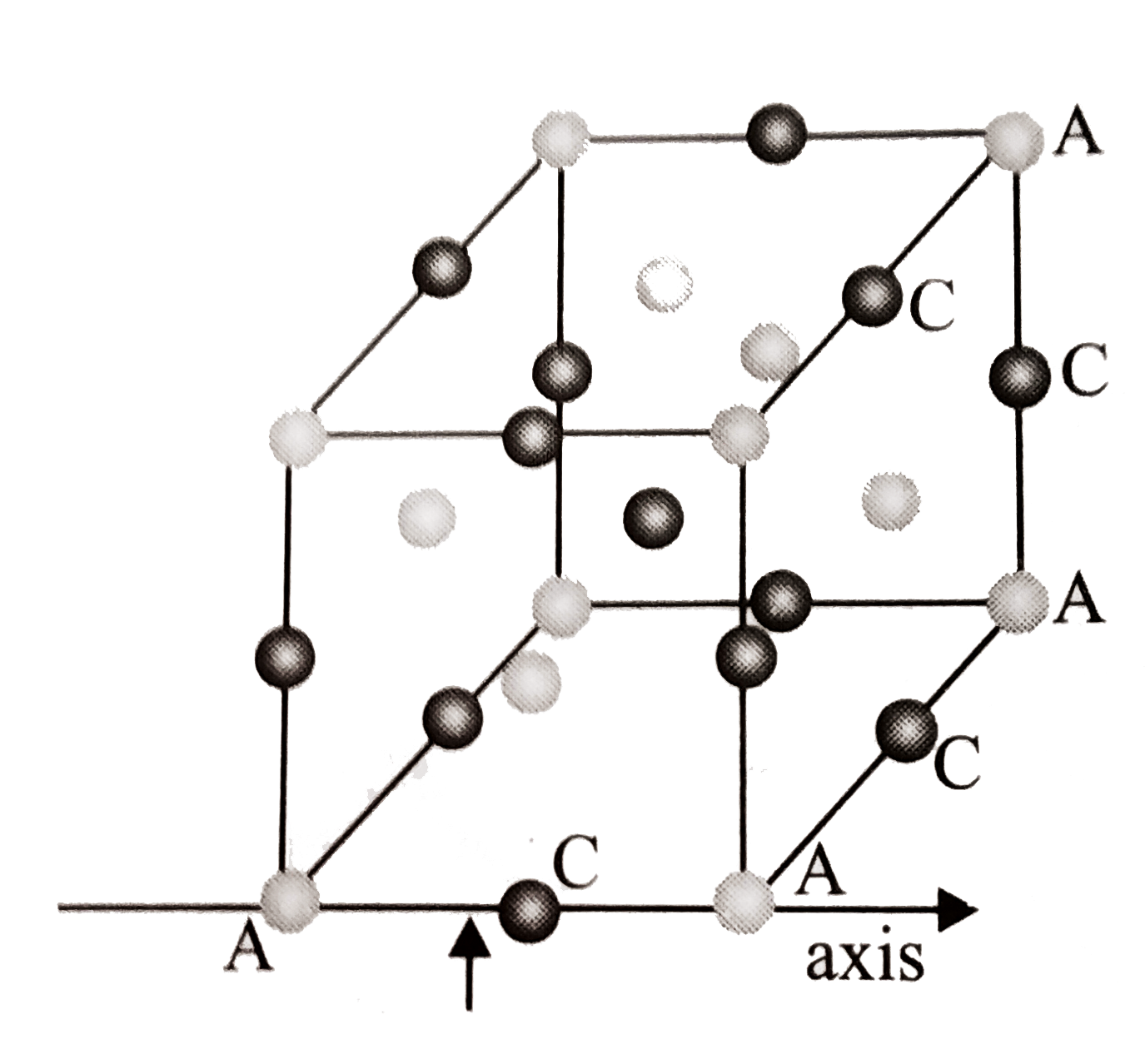
Class 12
CHEMISTRY
A compound made of particles A, B, and C...

A compound made of particles `A`, `B`, and `C` forms `ccp` lattice. Ions `A` are at lattice points, `B` occupy `TV_(s) C` occupy `OV_(s)`. If all the ions along one of the edge axis are removed, then formula of the compound is

A

`A_(3.75)B_(8)C_(3.75)`

B

`A_(3.75)B_(4)C_(8)`

C

`A_(4)B_(8)C_(3.75)`

D

`A_(4)B_(3.75)C_(8)`

Text Solution

Verified by Experts

The correct Answer is:
A
Since lattice is `ccp, Z_(eff) = 4`.
`:.` Number of `A` ions `= 4`
(corner `+` face centre `= 1 + 3 = 4`)
Number of `B` ions `=` Number of `TV_(s) = 8`
Number of `C` ions `=` Number of `OV_(s) = 4`
`2 TV_(s)` are founded at each diagonal of cube.
`4 TV_(s)` are founded on edge centres and body of centre.

`2 A` ions (at corners) and one `C` ion (at edge centre are removed.
Number of `A` ions removed `= 2 xx (1)/(8)` (corner share)
`= (1)/(4)`
Number of `C` ions removed `= 1 xx (1)/(4)` (edge centre share)
`= (1)/(4)`
Number of `A` ions left `= 4 - (1)/(4) = 3.75`
Number of `B` ions `= 8`
(Since no `B` ion has been removed)
Number of `C` ions left `= 4 - (1)/(4) = 3.75`
Thus, formula is: `A_(3.75)B_(8)C_(3.75)`
Promotional Banner

Similar Questions

Explore conceptually related problems

A compound made of particles A , B , and C forms ccp lattice. In the lattice, ions A occupy the lattice points and ions B and C occuphy the alternate TV_(s) . If all the ions along one of the body diagonals are removed, then formula of the compound is

A compound made of particles A and B . A forms fc c packing and B occupies all the OV_(s) . If all the particles along the plane as shown in the figure below are removeed, then the simplest formula of the compound is

A crystal is made up of particals X , Y , and Z . X froms fcc packing. Y occupies all octahedral voids of X and Z occupies all tetrahedral voids of X . If all the particles along one body diagonal are removed. Then the fromula of the crystal would be

Three element A,B and C crystallise into a cubic solid lattice. Atoms A occupy the corners, B occupy the cube centres and C occupy the edges. The formula of the compound is :

In a face centred cubic lattice, atom A occupies the corner positions and atom B occupies the face centre positions. If one atom of B is missing from one of the face centred points, the formula of the compound is :

A solid is made up of two elements P and Q. P atoms are in ccp arrangement while atoms Q occupy all the octahedral voids and half of the tetrahedral voids. The formula of the compound is :

A compound A_(x)B_(y) crystallises on a fcc lattice in which A occupies each corner of a cube and B occupies the centre of each face of the cube. What is the formula of the compound ?

In a compound, atoms of element Y form ccp lattice and those of X occupy 2//3 rd of tetrahedral voids. The formula of the compound will be :