Home
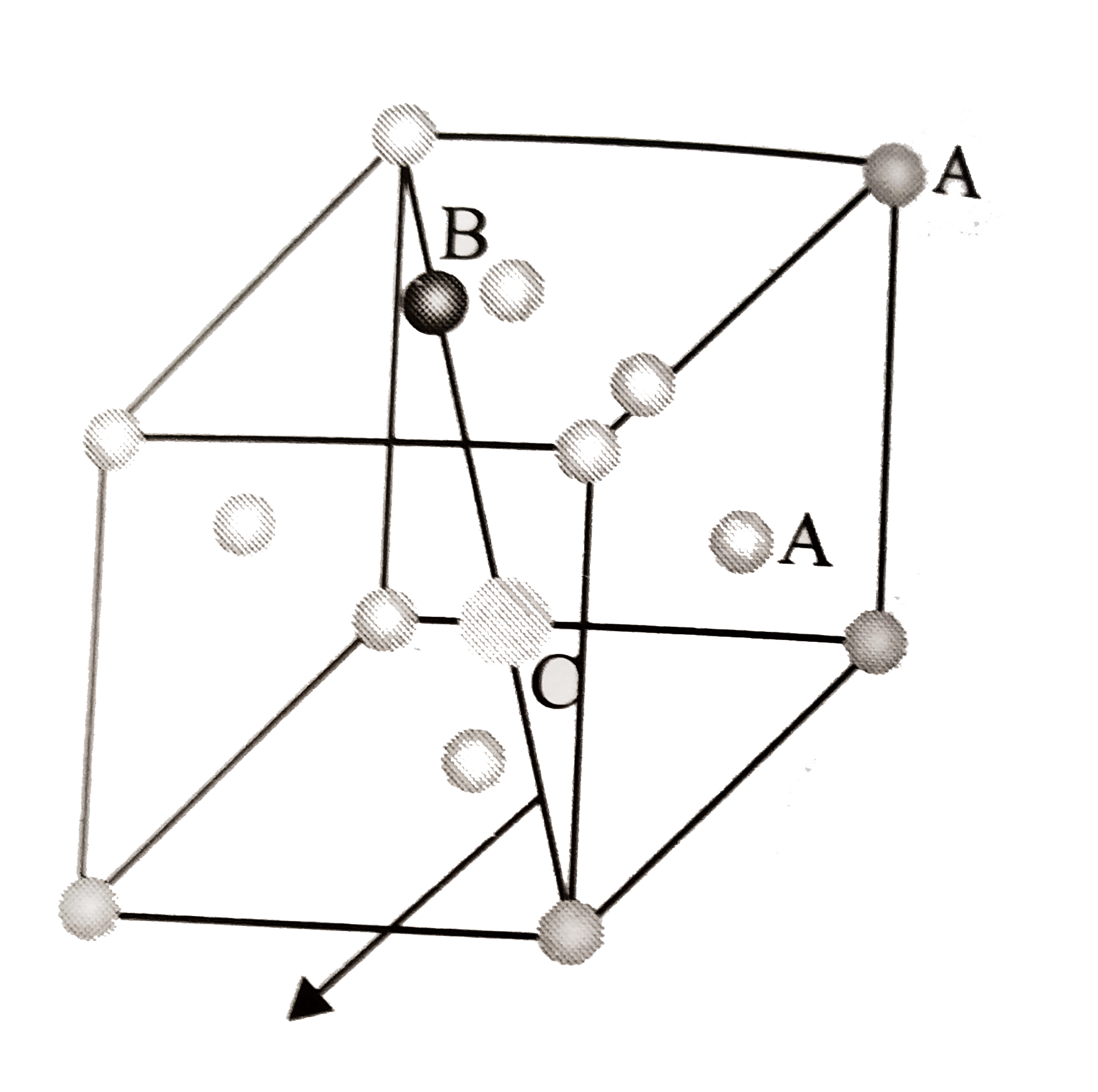
Class 12
CHEMISTRY
A compound made of particles A, B, and C...

A compound made of particles `A`, `B`, and `C` forms `ccp` lattice. In the lattice, ions `A` occupy the lattice points and ions `B` and `C` occuphy the alternate `TV_(s)`. If all the ions along one of the body diagonals are removed, then formula of the compound is

A

`A_(3.75)B_(3)C_(3)`

B

`A_(3.75)B_(3)C_(4)`

C

`A_(3)B_(3.75)C_(3)`

D

`A_(3)B_(3)C_(3.75)`

Text Solution

Verified by Experts

The correct Answer is:
A
a. Since the lattice is `c cp (Z_(eff) = 4)`.
`:.` Number of `A` ions `= 4`
(corner `+` face centre `= 1 + 3 = 4`)
Number of `B` ions `=` Number of alternate `TV = 4`
Number of `C` ions `=` Number of alternate `TV = 4`.
Number of `A` ions removed `= 2 xx (1)/(8)` (corner share)
`= (1)/(4)`

One of the body diagonals. Other diagonals are not shown in the figure
Number of `B` ions removed `= 1`
Number of `C` ions removed `= 1`
(Since body diagonal ions are inside the cube so they do not share with other ions).
Number of `A` ions left `= 4 - (1)/(4) = 3.75`
Number of `B` ions left `= 4 - 1 = 3`
Number of `C` ions left `= 4 - 1 = 3`
Thus, formula is: `A_(3.75)B_(3)C_(3)`
Promotional Banner

Similar Questions

Explore conceptually related problems

A compound made of particles A , B , and C forms ccp lattice. Ions A are at lattice points, B occupy TV_(s) C occupy OV_(s) . If all the ions along one of the edge axis are removed, then formula of the compound is

In a face centred cubic lattice, atom A occupies the corner positions and atom B occupies the face centre positions. If one atom of B is missing from one of the face centred points, the formula of the compound is :

A crystal is made up of particals X , Y , and Z . X froms fcc packing. Y occupies all octahedral voids of X and Z occupies all tetrahedral voids of X . If all the particles along one body diagonal are removed. Then the fromula of the crystal would be

A compound made of particles A and B . A forms fc c packing and B occupies all the OV_(s) . If all the particles along the plane as shown in the figure below are removeed, then the simplest formula of the compound is

A compound A_(x)B_(y) crystallises on a fcc lattice in which A occupies each corner of a cube and B occupies the centre of each face of the cube. What is the formula of the compound ?

A mineral having the formula AB_(2) crystallizes in the ccp lattice, with A atoms occupying the lattice points. Select the correct statement(s).

A compound A_(x)B_(y) crystallizes in a FCC lattice in which A occupies each corner of a cube and B occupies the centre of each face of the cube. What is the formula of the compound?

Three element A,B and C crystallise into a cubic solid lattice. Atoms A occupy the corners, B occupy the cube centres and C occupy the edges. The formula of the compound is :