A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
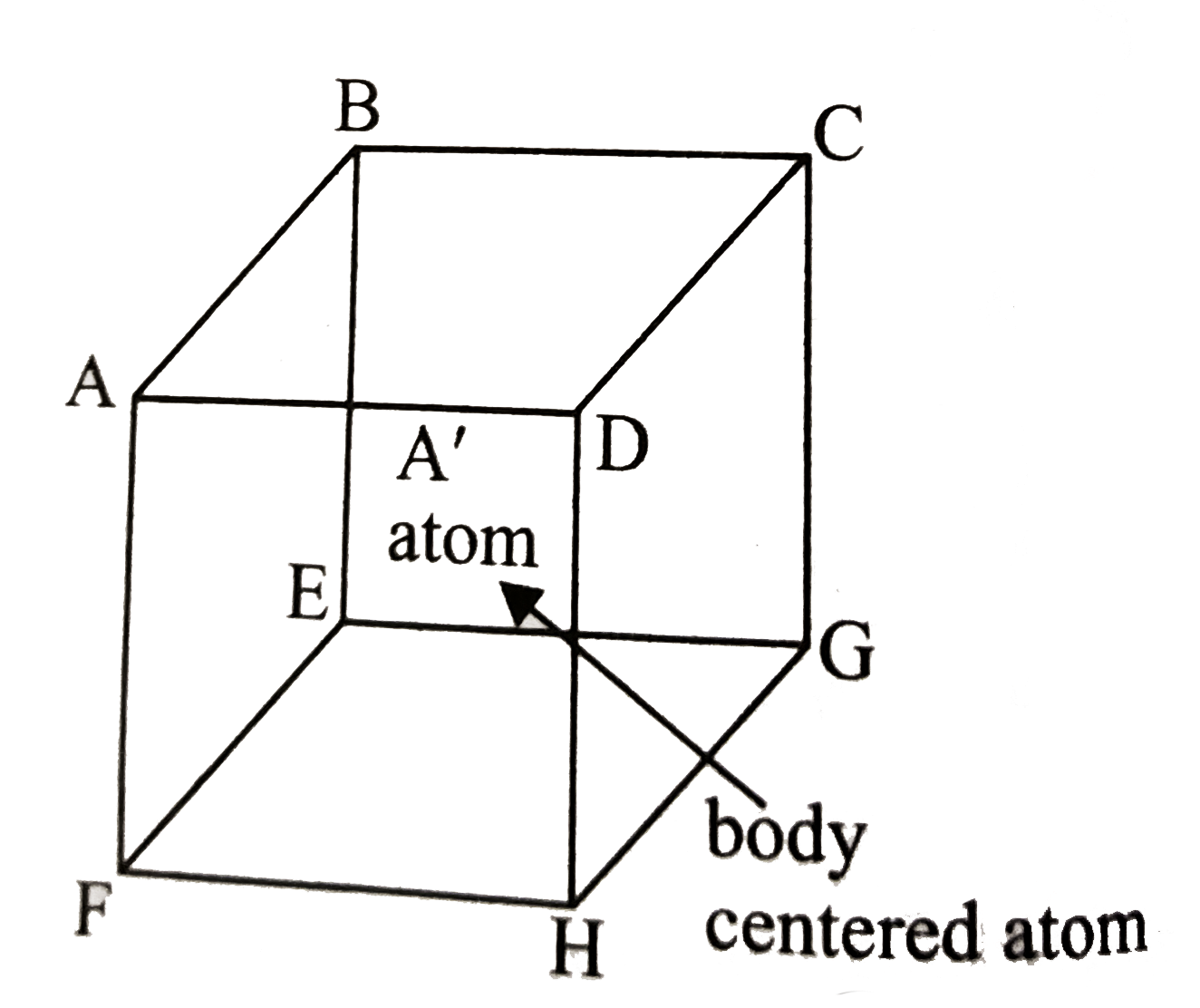
- In body-centred cubic lattice given below, the three disntances AB, AC...
Text Solution
|
- Body centred cubic lattic has a coordination number
Text Solution
|
- First three nearest neighbour distance for body centred cubic lattice ...
Text Solution
|
- Body -centred cubic lattice has a corrdination number of
Text Solution
|
- Body centred cubic lattice has a coordination number of
Text Solution
|
- Body -centred cubic lattice has a corrdination number of
Text Solution
|
- Body -centred cubic lattice has a corrdination number of
Text Solution
|
- Sketch the body centred cubic lattices.
Text Solution
|
- The three distances AB, AC and AA' in the given BCC lattice are :
Text Solution
|