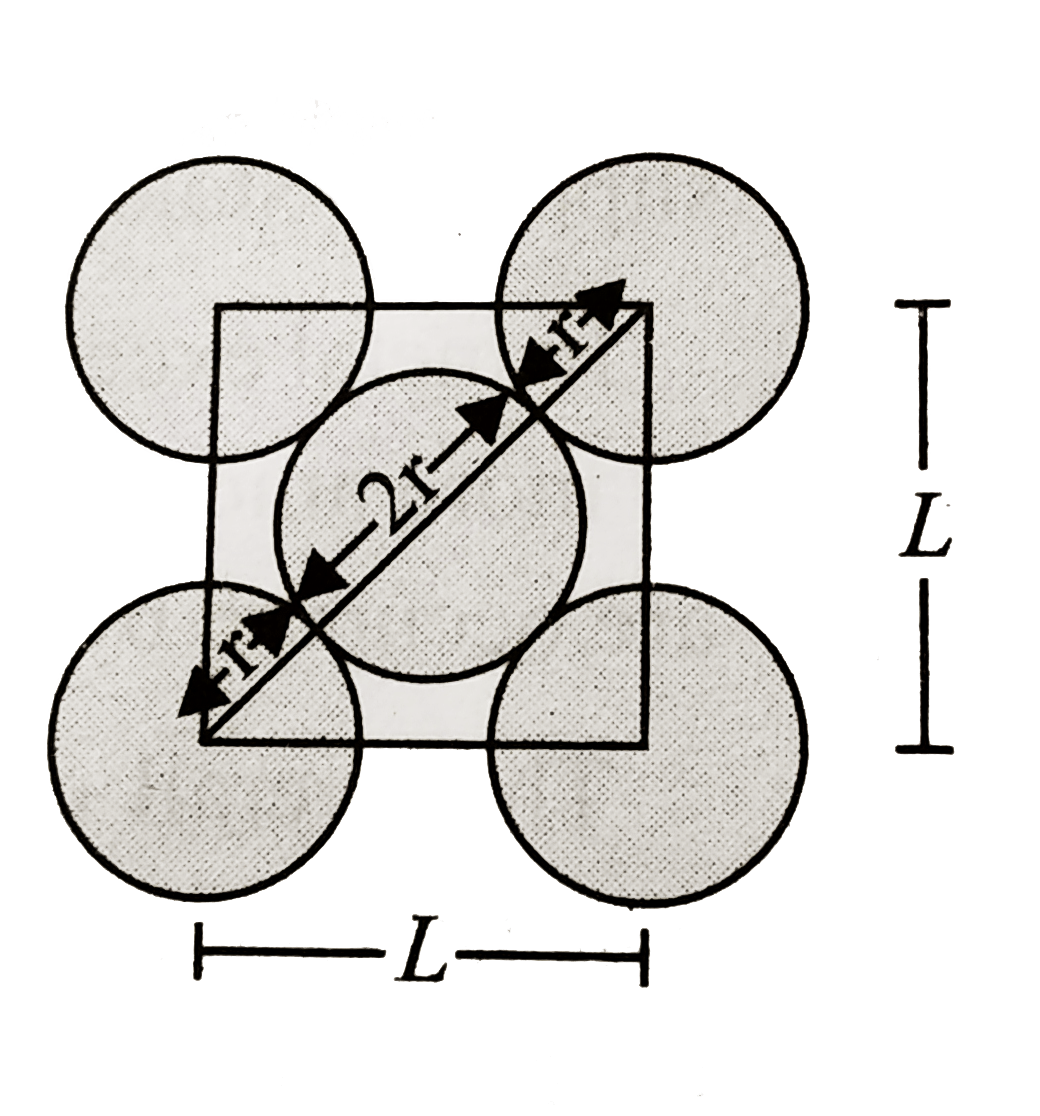
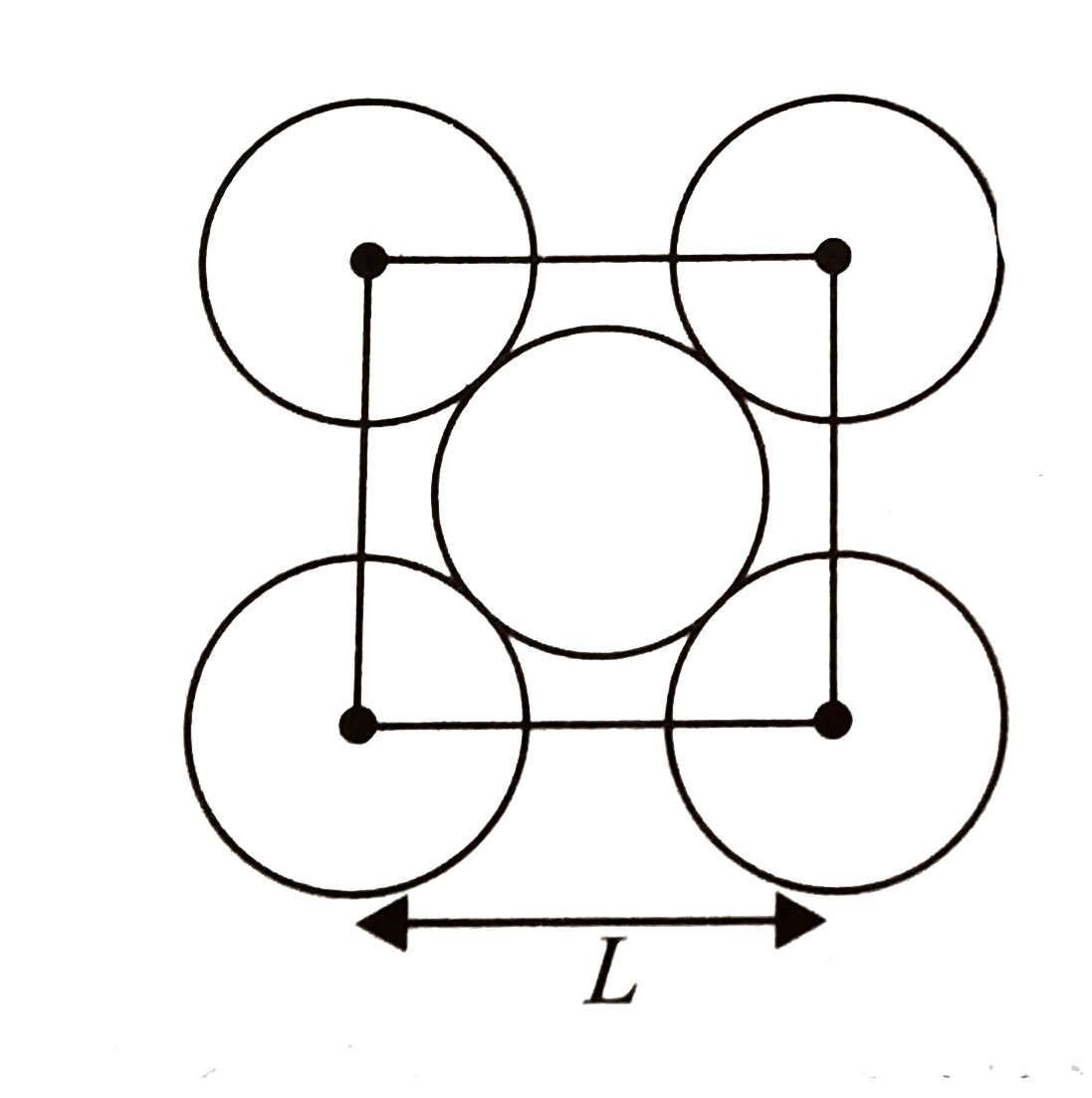A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The packing efficiency of a two-dimensional square unit cell shown bel...
Text Solution
|
- The packing efficiency of the two dimensional square unit cell shown b...
Text Solution
|
- The packing effciency of the two dimensional cell square unit as show...
Text Solution
|
- The packing efficiency of the two dimensional square unit cell show in...
Text Solution
|
- The packing efficiency of the two-dimensional sqare unit cell shown be...
Text Solution
|
- Calculate the packing efficiency of the two-dimensional square unit ce...
Text Solution
|
- The packing efficiency of the two - dimensional square unit cell show ...
Text Solution
|
- निचे दिए गए द्विविमीय वर्ग एकक सेल की संकुलन क्षमता है :
Text Solution
|
- The packing efficiency of the 2D square unit cell shown below is
Text Solution
|