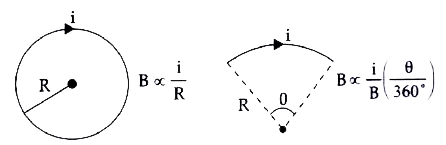
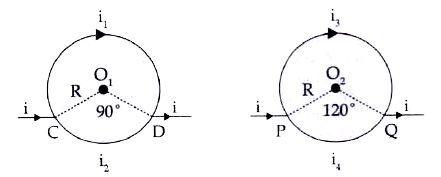
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Magnetic fieldn at the centre of a circular coil of radius R carrying...
Text Solution
|
- Plot a magnetic field due to a circular coil carrying current and expl...
Text Solution
|
- If current through a circular coil flows in clockwise direction, then ...
Text Solution
|
- A circular coil of radius R carries a current i . The magnetic field a...
Text Solution
|
- The magnetic induction at the centre of a current carrying circular of...
Text Solution
|
- {:(1.,"Right hand thumb rule",(a),"To find the direction of magnetic f...
Text Solution
|
- At what distance on the axis, from the centre for circular current car...
Text Solution
|
- Consider a circular conductor coil located on the table plane. Apply t...
Text Solution
|
- A current circular conducting loop exerts a magnetic field both inside...
Text Solution
|