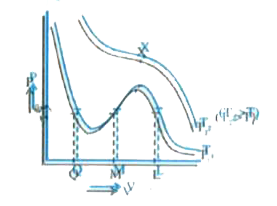
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- At a particular temperature and pressure for a real gas Van der Waal's...
Text Solution
|
- Find out the unit and dimensions of the constants a and b in the van ...
Text Solution
|
- The van der Waal's equation of state for some gases can be expressed a...
Text Solution
|
- The van der Waal's equation of state for some gases can be expressed a...
Text Solution
|
- The van der waal's gas equation is (P+a/V^(2))(V-b)=RT , where P is pr...
Text Solution
|
- The van der waal's gas equation is (P+a/V^(2))(V-b)=RT , where P is pr...
Text Solution
|
- The van der waal's gas equation is (P+a/V^(2))(V-b)=RT, where P is pre...
Text Solution
|
- The van der waal's gas equation is (P+a/V^(2))(V-b)=RT , where P is pr...
Text Solution
|
- The van der Waals' equation for one mole may be expressed as V(M)^(3...
Text Solution
|